Procura Local
Tal como referido na secção dos CSPs, a procura local é uma abordagem de procura que parte de uma configuração inicial completa, procurando encontrar uma configuração completa e consistente - de um modo mais geral, e procurando abstrairmo-nos do contexto dos CSPs, procuramos um estado objetivo, realizando transições sucessivas entre "estados vizinhos". Tem, claro, ganhos quanto à sua complexidade espacial, em comparação com a procura sistemática habitual: em vez de termos de guardar uma árvore de procura, vamos apenas guardando uma configuração do problema que se vai alterando com o passar do tempo. Contudo, e como there's no such thing as a free lunch, estes ganhos em memória traduzem-se na incapacidade de saber o caminho que leva uma configuração "vazia" do problema a uma solução - esta forma de procura é, portanto, ideal para cenários onde o caminho é irrelevante, onde apenas queremos saber se existe uma solução possível (e, se sim, qual). Correm também o risco de ficar facilmente presas em ciclos, não sendo, portanto, completas nem ótimas com implementações normais.
A ausência de otimalidade é relativamente simples de compreender: se um estado tiver um dado valor objetivo e todos os seus vizinhos tiverem valores objetivo inferiores a (considerando, claro, que o objetivo é maximizar esse valor), o algoritmo fica sem saber para onde ir, parando ali, mesmo que eventualmente exista outro estado com valor objetivo maior. O gráfico abaixo ilustra de forma clara este problema: através da procura local, conseguimos encontrar de forma rápida máximos locais, mas não é garantido que encontremos o máximo global, a configuração ótima pretendida:
Note-se como, olhando para o estado atual, e considerando que a cada momento temos apenas dois vizinhos (o estado "à esquerda" e o "à direita"), vamos acabar sempre por ir para a direita, efetivamente afastando-nos do estado ótimo. Assim que chegamos ao máximo local, os respetivos estados à esquerda e à direita têm ambos valores objetivo menores, pelo que a procura é suspensa aí, num máximo local que não é o máximo global.
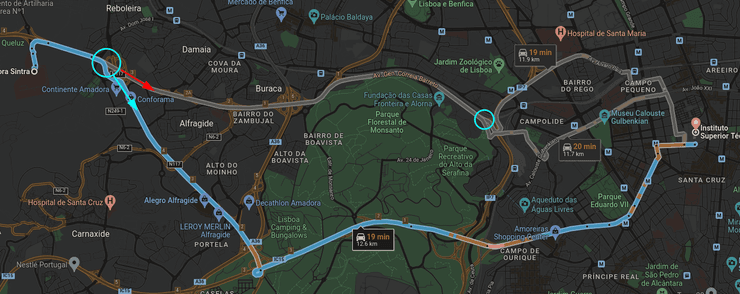
Em relação a cenários práticos onde a procura local possa ser utilizada como aliada da procura global, pensemos, por exemplo, num cenário de GPS, onde uma procura global conseguiu encontrar o caminho mais curto entre duas localidades. O motorista começou a sua viagem, e a meio ocorre um acidente que corta uma das estradas que o caminho mais curto utilizava - aqui, a procura local pode ser particularmente útil, já que, partindo de um estado inicial completo, bastará, em princípio, alterar pouco a rota em vez de ter de realizar uma nova procura global.
Na imagem acima, podemos ver dois pontos onde a rota se podia alterar facilmente - se houvesse um acidente ao pé do Alegro Alfragide, o GPS deveria recalcular a melhor rota. Em vez de fazer uma procura global de novo para o fazer, pode escolher estados "vizinhos", tal como a rota demarcada com a seta vermelha!
Procura Hill Climbing/Local Gananciosa
Funciona tal e qual foi referido mais acima: uma procura que escolhe sempre o estado com maior valor objetivo de entre os seus vizinhos, terminando quando nenhum deles tem valor melhor que o dele próprio. O nome vem precisamente da forma como se comporta: esta abordagem procura sempre "trepar a colina mais inclinada que consegue ver", considerando, claro, que só consegue ver o que está imediatamente à sua frente.
function hill_climbing(problem)
current_state = problem.initial_state
while true do
# se houver mais que um vizinho com valor objetivo máximo,
# a escolha é feita de forma aleatória
neighbor = current_state.get_highest_valued_neighbor()
if neighbor.value <= current_state.value then
return current_state
current_state = neighbor
doneNote-se, mais uma vez, como a procura hill climbing sofre o problema de poder parar em máximos locais, ignorando outros máximos que existam (possivelmente com valor maior do que aquele onde está):
* Voltando a pegar na questão da completude, o nosso estado final pode até não corresponder a uma solução admissível, caso apenas o máximo global corresponda a uma solução admissível: no exemplo das rainhas ilustrado abaixo, chegamos a uma situação onde qualquer movimento que façamos leva a que mais rainhas se ataquem (no momento imediatamente seguinte), pelo que a procura termina, e terminámos sem uma solução consistente!
Uma estratégia para contornar o problema dos máximos locais nesta procura
consiste em alterar ligeiramente o pseudo-código do mesmo: passar de
if neighbor.value <= current_state.value then para if neighbor.value < current_state.value then,
podendo, assim, "atravessar planaltos". Surgem, contudo, outros problemas: podemos
facilmente entrar em ciclos (combatidos colocando um limite no número de sideways moves,
por exemplo), e, claro, continua sem haver garantia de encontrar a solução pretendida.
Variações - Hill Climbing
Sendo hill climbing uma das abordagens clássicas para procura local, surgiram, inevitavelmente, várias maneiras de a tentar melhorar.
Stochastic Hill Climbing
Em vez de escolher sempre o estado com maior valor objetivo de entre os vizinhos com valor objetivo maior que o seu, vamos, aqui, escolher um estado de forma aleatória de entre esse mesmo grupo de vizinhos - deixa de ser uma escolha gananciosa, já que não vamos sempre escolher o estado com maior valor objetivo, passando a ser estocástica (ligada à sorte, portanto).
First-Choice Hill Climbing
Em vez de gerar todos os sucessores de uma vez e escolher o vizinho entre o conjunto de todos os vizinhos com valor objetivo maior que o próprio, vamos, aqui, gerar os sucessores de forma aleatória, um de cada vez, e escolher o primeiro com valor objetivo maior que o que já temos. Poupa, claro, tempo de processamento (visto que, por norma, há uma grande quantidade de sucessores que nunca é gerada), sendo, portanto, ideal para espaços de estados onde cada um tem uma quantidade relativamente grande de vizinhos.
Note-se que nenhuma das abordagens referidas até agora resolve o problema do algoritmo poder parar em máximos locais.
Ora, uma maneira interessante de contornar este problema seria, por exemplo, a aleatoriedade: visto que vamos sempre iniciar a procura com uma configuração inicial aleatória, se o fizermos vezes suficientes é bastante provável que cheguemos à solução pretendida. Houve estudos realizados para o problema das rainhas, precisamente para tentar perceber se esta abordagem valeria ou não a pena. Descobriu-se que, em média, partindo de uma configuração inicial arbitrária:
- se hill climbing for encontrar uma solução, fá-lo-á em cerca de passos;
- se for ficar preso num ciclo, tal acontecerá em cerca de passos.
Podemos, assim, "parar a procura" (tanto artificialmente como ao chegar a uma solução) bastante rápido, pelo que vale a pena repetir a procura várias vezes, com configurações iniciais distintas, por forma a tentar obter a solução pretendida.
Tem-se que esta variante, a random-restart hill climbing, é completa para uma probabilidade próxima de - quanto mais vezes for repetida, maior a probabilidade de encontrar a solução. Considerando como a probabilidade de sucesso de cada procura, vamos (em princípio) precisar de cerca de tentativas para encontrar a solução. Considerando, por exemplo, o problema das rainhas que converge para solução (ou fracasso) bastante rápido, esta abordagem parece excelente: apesar de não garantir, em teoria, completude, na prática é raríssimo que, com um número suficiente de tentativas, não encontremos a solução.
Simulated Annealing
Na área da metalurgia, annealing corresponde ao processo de endurecer um metal, colocando-o primeiro a temperaturas muito altas, procurando de seguida arrefecê-lo gradualmente. O método descrito abaixo, simulated annealing, acaba por corresponder a uma implementação de uma metáfora semelhante no contexto da procura local (bem, igual, só que diferente). Pensemos num cenário em que queremos que uma bola chegue ao fundo de um "vale" com aspeto parabólico, vale esse com paredes particularmente pegajosas (às quais a bola pode facilmente prender-se):
Se abanarmos vezes suficientes o vale, mesmo que a bola vá ficando presa em "mínimos locais" (leia-se, fique pegada às paredes do vale) sucessivos, eventualmente vamos conseguir fazer com que chegue lá abaixo. A procura por simulated annealing baseia-se nisso mesmo: em tentar fazer com que os estados saiam de máximos/mínimos locais, "abanando-os". "Abanar" os estados consiste, aqui, em escolher (por vezes) estados com valor objetivo pior do que o que temos atualmente, por forma a procurar sair de máximos/mínimos locais em direção ao global. Esta escolha é feita da seguinte maneira:
- se gerarmos um vizinho com valor objetivo maior que o que temos atualmente, escolhemo-lo, no questions asked;
- caso geremos um vizinho com valor objetivo menor que o que temos atualmente, existe a possibilidade de o escolhermos na mesma: temos, contudo, de ter cuidado para não nos afastarmos demasiado dos extremos locais que já encontrámos, ficando ainda mais longe de encontrar extremos globais, pelo que a probabilidade (sempre menor que ) de escolher estes vizinhos diminui à medida que o movimento se aproxima cada vez mais dos extremos globais - isto é, se nos estivermos a aproximar "do que queremos", não faz tanto sentido ir noutra direção como fazia inicialmente, quando estávamos longe e qualquer abanão podia surtir efeitos positivos.
Local Beam Search
A procura local surge, de uma forma geral, como alternativa à procura global, principalmente no que à memória diz respeito. Ora, mas passar de memória exponencial para constante ainda é um salto relativamente grande: não haverá um meio termo que nos beneficie mais? Bem, é a partir deste pensamento que surge a procura local em banda, um compromisso intermédio entre as duas abordagens.
Optamos, aqui, por gerar estados iniciais, todos eles aleatórios. Se algum deles for estado-objetivo, paramos. Caso contrário, vamos ver todos os vizinhos dos estados, e escolhemos os * melhores estados, entre todos os vizinhos que gerámos. Este processo é realizado iterativamente até que encontremos um estado-objetivo.
* Note-se que caso um dos estados, seja ele , gere vizinhos fantásticos e todos os outros, para todos os outros estados, sejam medíocres, não vamos apenas escolher vizinho por estado: vamos escolher os vizinhos de , e depois outros vizinhos entre o resto dos medíocres.
Procura Local em Banda Estocástica
Podemos, eventualmente, chegar a situações em que os estados que temos em mãos são pouco diversos - tal pode acontecer, por exemplo, num espaço de estados relativamente pequeno (e/ou denso), em que facilmente conseguimos ficar "presos" a um conjunto parco de bons estados. Para nos ajudar a combater este problema, existe a variante estocástica da procura local em banda, onde em vez de escolhermos sempre os melhores vizinhos dos estados atuais, escolhemos vizinhos de forma estocástica - vamos aqui, considerar que quanto "melhor" for o vizinho, maior a probabilidade de ser escolhido, contudo sem qualquer garantia de tal acontecer. A médio-longo prazo, esta abordagem permite uma maior diversidade no conjunto de estados que vamos explorando!
Algoritmos Genéticos
Correspondem a algoritmos baseados na procura em banda estocástica, referida acima, e na ideia da "seleção natural" associada à genética. Começamos com uma população inicial, com estados (ou indivíduos). Estes indivíduos vão eventualmente reproduzir-se, por forma a dar continuidade à espécie (leia-se, vamos gerar os estados vizinhos), e eventualmente vamos gerando indivíduos "melhores", tal como dita a teoria da evolução - as mutações positivas mantêm-se, da mesma maneira que vamos sempre procurar estados que estejam a "ir na direção certa". Esta noção de estados melhores e piores pode ser quantificada segundo uma função, a fitness function, onde os melhores estados recebem os valores mais altos: the fittest individuals stay alive. Vamos cruzando estados pais, mantendo propriedades iguais entre os mesmos, procurando ainda verificar se certas alterações levam ou não a resultados melhores, em busca do "indivíduo perfeito": a solução pretendida, o estado que corresponde a uma solução.
Este tipo de algoritmos pode, ainda, variar considerando várias componentes:
- O tamanho da população pode, claro, ser infinitamente variável;
- A representação de um estado é também arbitrária: tanto podemos ter strings sobre alfabetos , como qualquer alfabeto numérico, entre outros;
- A quantidade de "pais" - acima foram referidos dois pais, mas podemos ter um (sendo essa abordagem a procura em banda estocástica clássica) ou mesmo mais que dois pais;
- O próprio processo de seleção, que não tem necessariamente de ter uma relação direta com a fitness function (podendo ser mais aleatório), entre outras.
Tomemos novamente o exemplo das rainhas, contando com configurações iniciais. Aqui, cada estado corresponde a uma string com comprimento , onde cada dígito corresponde à linha onde a rainha da coluna em questão está colocada. O valor da fitness function associado a cada estado corresponde ao número de pares de rainhas que não se atacam, onde, claro, valores maiores correspondem a estados melhores, visto que, no fim, queremos que nenhum par se ataque.
Podemos ver que foram escolhidos, de forma aleatória, dois pares de estados para cruzamento. Escolhemos ainda que partes da string se vão cruzar, escolha esta igualmente aleatória. Cruzamos, então, os estados, gerando quatro novos estados. Por fim, podemos (ou não) aplicar mutações aos estados gerados, adicionando-lhes, assim, mais uma camada de aleatoriedade.
O livro que acompanha a cadeira inclui esta passagem, bastante interessante no que toca a este tema:
The theory of genetic algorithms explains how this works using the idea of a schema, which is a substring in which some of the positions can be left unspecified. For example, the schema 246***** describes all 8-queens states in which the first three queens are in positions 2, 4, and 6, respectively. Strings that match the schema (such as 24613578) are called instances of the schema. It can be shown that if the average fitness of the instances of a schema is above the mean, then the number of instances of the schema will grow over time. Clearly, this effect is unlikely to be significant if adjacent bits are totally unrelated to each other, because then there will be few contiguous blocks that provide a consistent benefit. Genetic algorithms work best when schemas correspond to meaningful components of a solution. For example, if the string is a representation of an antenna, then the schemas may represent components of the antenna, such as reflectors and deflectors. A good component is likely to be good in a variety of different designs. This suggests that successful use of genetic algorithms requires careful engineering of the representation.
Como recurso adicional, a seguinte playlist cobre esta secção da matéria:
Procura Local em Espaços Contínuos
Página em construção
O conteúdo será adicionado assim que possível.
Procura com Ações Não Determinísticas
Em cenários reais, as nossas ações podem ter mais do que um resultado possível: se um indivíduo particularmente descoordenado tentar rematar uma bola de futebol, por exemplo, a bola pode não ir exatamente para onde ele quer (apesar de haver a possibilidade de tal acontecer). Esta é, claro, a ideia-base por detrás do não determinismo, questão sobre a qual nos vamos debruçar de seguida.
Podemos tentar ilustrar esta ideia através do exemplo do aspirador que utilizámos na secção dos agentes: considerando um estado inicial, em que o aspirador está na posição e essa mesma posição está suja, a ação "aspirar" pode nem sempre resultar na mesma transição:
- O aspirador pode avariar-se de repente, e não aspiramos nada;
- Podemos aspirar, sem querer, a posição (para além de ).
Vamos, portanto, ter de adaptar a nossa noção de modelo de transição, passando esta a retornar um conjunto de estados que podem resultar de aplicar uma ação a um estado . Tratam-se, portanto, de cenários não determinísticos.
Como realizar procuras em cenários não determinísticos
Surge então uma questão pertinente - em cenários onde não é possível prever com exatidão o resultado de uma dada ação, como é que é suposto fazermos procuras corretas? Bem, sabemos sempre que, partindo de qualquer estado, podemos construir o conjunto das ações realizáveis a partir dele. Mais ainda, sabemos que, se a ação é realizável, então terá um conjunto de estados resultantes de realizar a ação partindo de um estado . Começa aqui a formar-se uma ideia quase cíclica: partimos de estados, temos um conjunto de ações que podemos tomar, e realizando essas ações podemos ir parar a um conjunto de outros estados, ideia esta que não parece nova (e de facto não é - temos, contudo, de precaver outcomes diferentes para uma mesma ação). Esta ideia traduz-se, na prática, numa árvore AND-OR: uma árvore com dois tipos de nós, onde:
- os nós OR correspondem a ações: a ação "aspirar", por exemplo, corresponde a um nó OR válido;
- os nós AND correspondem a estados.
A lógica por detrás destas árvores é, então, simples de entender: partindo de nós AND, vemos que ações podemos executar a partir deles, e geramos os nós correspondentes (que vão ser seus filhos) - os nós OR. Posteriormente, verificamos os estados resultantes de aplicar a ação em OR ao pai AND, e daí resultam os filhos de OR: os tais estados resultantes, um conjunto de nós AND. A árvore correspondente ao cenário do aspirador podia, então, ser representada da seguinte forma:
Neste tipo de árvores, todas as folhas são objetivos. Mais ainda, caso encontremos um estado repetido seguindo um dado caminho, podemos dizer que entrámos em ciclo, retornando failure.
Existem, contudo, cenários onde temos de utilizar ciclos para atingir a solução pretendida: caso apenas nos falte uma posição por limpar, por exemplo, e a nossa tentativa de aspirar essa posição falhar, vamos inevitavelmente entrar em ciclo. A solução passa, nestas circunstâncias, por tentar repetidamente aspirar, até finalmente conseguir! Depreende-se, então, que ciclos causados "aleatoriamente" são aceitáveis, como o do exemplo ainda agora referido, e que qualquer outro tipo deve ser rejeitado.
Procura em Ambientes Parcialmente Observáveis
Na vida real, nem sempre vamos conhecer por completo o nosso meio envolvente - tal como referido no início da secção de resumos de IA, este tipo de ambiente diz-se parcialmente observável. Vamos, portanto, debruçar-nos sobre estratégias que procurem remover alguma da camada de incerteza que vai estar associada a este tipo de cenários, estratégias essas que assentam na ideia da ausência de sensores: se o nosso agente não precisar de saber exatamente qual é o ambiente que o envolve, consegue trabalhar melhor em cenários mais complicados.
A nossa procura vai tratar, em vez de um conjunto de estados palpáveis/completamente observáveis, de um conjunto de crenças do agente. Tem um conjunto de componentes diferente do que foi visto até agora:
-
Um conjunto de estados, o espaço de crenças: contém todos os subconjuntos de estados físicos do problema original;
-
Um estado inicial - por norma, encontra-se inicialmente cheio, já que, na pior das hipóteses, não temos qualquer informação sobre o que nos rodeia (tendo, portanto, de considerar qualquer cenário como possível). Na prática, costumamos ter algumas pistas quanto ao estado inicial;
-
Um conjunto de ações, que corresponde ao conjunto de todas as ações que podemos fazer partindo de qualquer um dos estados do espaço de crenças;
-
Um modelo de transição, que difere entre as versões determinista e não-determinista. Num problema , para uma dada crença , a versão determinista dita que a crença , resultante de aplicar uma qualquer ação será dada por:
Por outro lado, a versão não-determinista dita que:
O modelo de transição tem três etapas: inicialmente, a fase da previsão, onde vai calcular as crenças resultantes da ação que vai tomar. De seguida, caso esteja num ambiente parcialmente observável, utiliza os seus sensores e a informação obtida para atualizar o seu espaço de crenças.
-
O teste objetivo, que aqui tem um senão: só é garantido que estamos no objetivo se todo o nosso espaço de crenças assim o afirmar - isto é, se todos os estados do nosso espaço de crenças satisfizerem o objetivo; caso contrário, possivelmente alcançámos o objetivo, sem qualquer garantia.
Abaixo, ilustra-se ainda o exemplo do modelo de transição num cenário em que o nosso agente tem sensores: aqui, vai conseguir olhar para o meio que o envolve e remover algumas crenças que afinal não têm cabimento.
Podemos, claro, aplicar a procura AND-OR a este tipo de cenários:
Procura Online - Ambientes Desconhecidos
Quando não conhecemos o ambiente que nos envolve, e existem penalizações (sejam elas artificiais ou naturais) por tempos de computação demasiado longos, pode fazer sentido intervalar a procura com ações, em vez de seguir sempre a mesma linha de procura até agora abordada: observamos o ambiente atual e o que sabemos sobre ele, calculamos a próxima ação a tomar por forma a atingir mais rapidamente o objetivo, e executamos essa mesma ação. Pensemos num caso mais extremo: queremos fugir de um labirinto, e temos uma quantidade limitada de tempo para o fazer. Nem sempre vamos ter tempo para parar e pensar, até porque muitas vezes não temos informação útil com que raciocinar: devemos, nessas circunstâncias, procurar navegar o desconhecido, por forma a recolher informação. Estamos, claro, bastante vulneráveis a encontrar becos sem saída, já que esta navegação consegue assemelhar-se, de vez em quando, a uma procura às cegas.
Note-se que esta abordagem tem particular utilidade no âmbito da exploração - é bastante provável que um agente, procurando às cegas, chegue ao fim tendo procurado a vasta maioria do ambiente que o envolve. Quanto à velocidade a que chega ao objetivo, contudo, é obviamente pior: uma procura pensada, em que conhecemos o ambiente e podemos prever o resultado das nossas ações tem todo um outro nível de "curadoria" que nos permite chegar mais eficientemente ao objetivo.
Abordámos, sem saber, um tipo de procura (local) cega mais acima: hill climbing, se pensarmos bem, mantém apenas informação sobre os seus vizinhos diretos, e não tem noção do meio que o envolve sem ser o que imediatamente o rodeia. Podemos, contudo, adicionar memória a hill climbing, por forma a tornar esta procura mais inteligente: guardamos uma estimativa de quanto custa chegar ao objetivo, partindo de cada estado que já foi visitado. Note-se, claro, que inicialmente cada nó tem uma heurística arbitrária:
O agente, aqui, utiliza o que sabe sobre a sua envolvência e, enquanto explora, vai guardando a nova informação sobre o ambiente que o rodeia. Assim que se apercebe que pode seguir um caminho melhor que o anterior, escolhe-o. A esta procura, hill climbing com memória, dá-se também o nome de Learning Real-Time , . Dizemos que opera segundo o princípio de otimismo sob incerteza: ao contrário da versão clássica de hill climbing, aqui o agente é encorajado a explorar o ambiente que o rodeia.
Adicionamos que esta secção corresponde ao quarto capítulo do livro que acompanha a cadeira (Search in Complex Environments).