Máquinas de Turing
Formalmente, uma máquina de Turing é um tuplo em que:
- é um alfabeto de trabalho, que inclui um símbolo , a que damos o nome de símbolo vazio;
- é um alfabeto de entrada/saída, ;
- é um conjunto de estados de controlo;
- é um estado inicial;
- são dois estados denominados estado de aceitação e estado de rejeição, respetivamente. Ambos estes estados dizem-se estados de terminação. Denominamos ;
- é uma função de transição.
Uma máquina de Turing deve ser entendida da seguinte forma:
Temos uma fita com posições que "guardam" símbolos num alfabeto - o alfabeto de entrada/saída.
Esta fita é infinita para a direita.
À medida que vamos fazer a nossa computação, podemos substituir os símbolos na fita com símbolos num alfabeto - o nosso alfabeto de trabalho.
O símbolo representa uma posição na fita vazia.
Note-se que , ou seja, o alfabeto de trabalho pode ter símbolos que não estão no alfabeto de entrada de saída. Então, podemos usar símbolos à nossa vontade para representar posições que nos sejam convenientes.
Temos um conjunto de estados de controlo . Tal como nos AFD's e AFND's, este será o nosso mecanismo principal de memória. Isto vai ser mais claro à frente.
O estado é, como nos autómatos, o estado em em que começamos as transições.
Os estados de aceitação e rejeição indicam se a nossa computação foi sucedida ou não.
Isto é, se criarmos uma máquina de Turing para resolver um dado problema, o nosso problema tem resposta afirmativa se chegar a um estado aceitação, e negativa se chegar a um estado de rejeição.
Em ambos os casos, a computação termina nesse momento.
Para uma computação terminar, não necessita de ler todos os símbolos que estavam inicialmente na fita - basta apenas que a computação leve a um estado terminação.
A função atua sobre a fita, e sobre o conjunto de estados:
- na fita:
- lemos um símbolo, que podemos substituir por outro símbolo em ;
- andamos para a esquerda () ou direita ().
- no conjunto de estados:
- transitamos tal como fazíamos nos autómatos.
Este mecanismo é um modelo computacional que nos permite fazer vários tipos de computação, nomeadamente:
- reconhecer uma linguagem - aceitar as suas palavras;
- decidir uma linguagem - aceitar as suas palavras e rejeitar as restantes;
- calcular uma função - aceitar inputs num certo domínio e calcular o respetivo output para esses inputs.
Para perceber exatamente como uma máquina de Turing funciona, vamos ver um exemplo.
Exemplo 1 - Reconhecimento de Linguagem
Começamos por um exemplo muito simples. Na verdade nem é necessária uma máquina de Turing para reconhecer esta linguagem, pelo que este exemplo é puramente ilustrativo.
Considere-se a linguagem formada pelas palavras sobre o alfabeto que são alternantes, isto é, em que cada símbolo (sem ser o primeiro) é diferente do que o antecede.
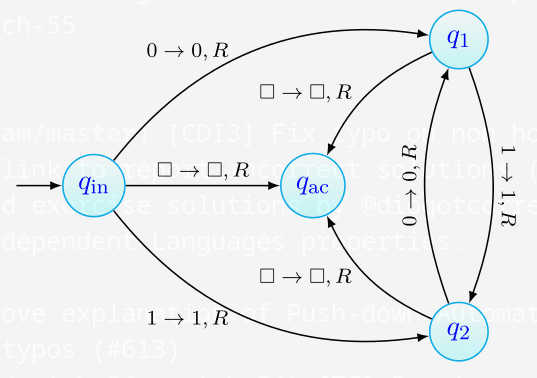
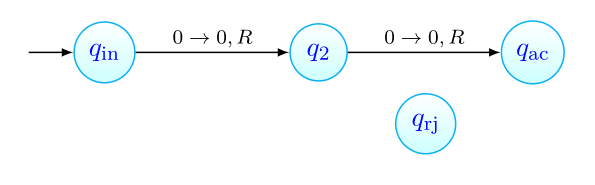
A seguinte máquina de Turing reconhece a linguagem:
A intuição por detrás da máquina é simples:
A partir do estado inicial, lendo o input da esquerda para a direita, a máquina transita para quando lê 0, memorizando dessa forma que o próximo símbolo a ler terá de ser 1, e para quando lê um 1, registando que o próximo símbolo a ler deve ser 0.
A máquina vai então alternando entre os estados e até processar todo o input, o que acontece quando é lido um espaço.
Neste momento, a computação vai para o estado de aceitação, terminando.
Caso dois símbolos consecutivos sejam iguais, a computação fica indefinida, já que não está representada nenhum transição a partir de quando o símbolo lido é 0, nem a partir de quando o símbolo lido é 1.
Exemplo 2 - Decisão de Linguagem
No exemplo 1 usamos, para além dos estados usamos apenas o estado de aceitação, pois estávamos apenas interessados em reconhecer a linguagem. Para decidir a linguagem, basta então adicionar um estado de rejeição e meter todas as transições não definidas do grafo anterior a apontar para lá.
Exemplo 3 - Cálculo de uma Função
Vamos continuar com a mesma linguagem. Queremos agora uma máquina de Turing que, em vez de reconhecer/decidir essa linguagem, tenha output 1 se o input for reconhecido pela linguagem e 0 caso contrário.
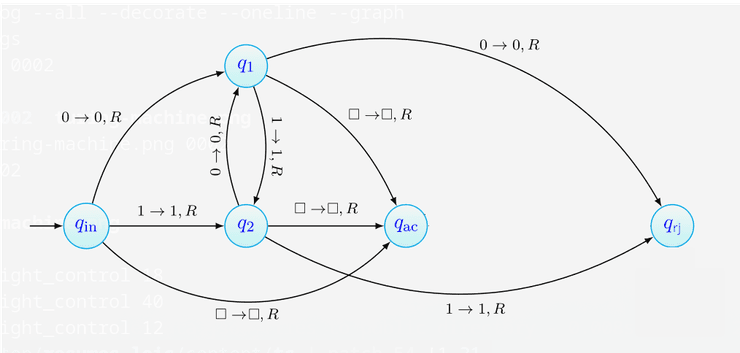
No exemplo anterior vimos a máquina de Turing para decidir a linguagem. A única diferença aqui é que queremos:
- quando uma palavra é aceite, imprimir 1 e terminar a computação no estado de aceitação;
- quando uma palavra não é aceite, imprimir 0 e terminar a computação no estado de aceitação na mesma (a nossa função completou com sucesso, pois reconheceu que a palavra não é aceite).
Para isso, substituímos os estados e por estados e respetivamente, que indicam que já sabemos o resultado da nossa computação. Neste ponto, para terminar a computação com sucesso basta então apenas imprimir o output adequado e ir para o estado de aceitação, como é feito abaixo.
Observe-se que o output deve ser imprimido só depois do input ser todo lido, pelo que no estado temos de ler o resto dos 0's e 1's.
Vamos agora formalizar aquilo que vimos nos exemplos acima.
Em cada momento, uma máquina de Turing está numa certa configuração. A configuração é determinada por:
- os símbolos na fita;
- a posição da cabeça de leitura/escrita;
- o estado em que a máquina se encontra.
Esta observação pode ser formalizada da seguinte forma:
Para uma máquina de Turing , definimos a sua configuração como o triplo em que é a palavra à esquerda da cabeça de leitura/escrita, é o estado corrente e a palavra que se inicia na cabeça de leitura/escrita e se prolonga para a direita até uma sequência infinita de células vazias.
Uma configuração diz-se de aceitação (resp., de rejeição) se o seu estado corrente for de aceitação (resp., de rejeição).
Observamos ainda que, para um input , a configuração inicial de uma máquina de Turing é sempre .
Definimos agora a função de transição de configurações de uma máquina de Turing tal que:
para quaisquer , , e .
Com esta definição, podemos então entender uma computação como uma sequência (finita ou infinita) de configurações.
Nomeadamente, a computação de uma máquina de Turing dado um input corresponde à sequência de configurações obtida a partir da configuração inicial usando transições de configuração .
Dizemos que a computação termina se sequência de configurações for finita, o que acontece se e só se for atingindo um estado de terminação (neste caso, a computação é bem sucedida) ou atingir uma configuração a partir da qual não está definida nenhuma transição (caso em que se diz que a computação aborta).
Se a computação não terminar, diz-se divergente.
Uma palavra diz-se aceite por se a computação que lhe é associada termina num estado de aceitação, e diz-se rejeitada se terminar no estado de rejeição.
Usamos , respetivamente, para denotar as linguagens aceite e rejeitada pela máquina de Turing .
Caso seja aceite por tal que é a configuração atingida pela computação, se com e , dizemos que é o output da computação e denotamos . A função denomina-se de função calculada por .
Dizemos que duas máquinas de Turing são equivalentes (representa-se ) se se verificarem 3 coisas:
- aceitam a mesma linguagem:
- rejeitam a mesma linguagem:
- calculam a mesma função:
Exemplo 4
Para oferecer um exemplo menos simples, vamos desenhar uma máquina de Turing que reconheça a linguagem sobre o alfabeto cujas palavras são palíndromos.
Num primeiro momento, é sempre importante verificar se a palavra vazia deve ser aceite - neste caso deve. Quando estamos na presença de um caso destes, normalmente temos de ter especial cuidado a construir a nossa máquina.
Pensemos: um palíndromo é uma palavra cuja palavra invertida é igual a si própria. Parece então fazer sentido ir verificando as pontas da palavra, verificando se coincidem. Essa verificação terá de ser feita consecutivamente, "podando as pontas" da palavra até dar a volta (verificando então que a palavra é um palíndromo) ou até as pontas não serem iguais (obtendo então que a palavra não é um palíndromo).
Este método de verificar e podar consecutivamente as pontas tem um defeito: por definição, não tem em conta palíndromos de comprimento ímpar - palavras onde eventualmente temos as pontas a "coincidir". Ao construir a máquina teremos, portanto, de ter esse caso em consideração (e já veremos abaixo que é uma modificação bastante simples à máquina).
Temos, então, a máquina de Turing que resolve o problema proposto acima. Podemos notar as tais transições auxiliares para palavras de comprimento ímpar referidas acima, partindo de e para . Em e , as iterações pela palavra até encontrar a próxima ponta, e em e o backtracking até à primeira ponta, marcada a última.
Acabamos, então, esta secção a exemplificar o processamento de um par de palavras segundo esta máquina:
Consideremos, como primeiro exemplo, a palavra . Partindo do estado inicial, o primeiro é lido, sendo substituído por na fita. Vamos, de seguida, iterar pela fita até encontrar a outra ponta da palavra - encontrada, verificamos que também é , pelo que até agora a palavra continua a poder ser um palíndromo. Marcamos esta ponta com e rebobinamos até à última ponta, e vamos agora passar a considerar a palavra . Marcamos com e prosseguimos até à próxima ponta. Descobrimos, aqui, que a outra ponta tem símbolo , pelo que a palavra definitivamente não é um palíndromo. Sem transição associada, a palavra é rejeitada pela máquina, e o processamento termina.
De seguida, tenhamos a palavra , palavra esta de comprimento ímpar. Vamos, mais uma vez, procurar sucessivamente marcar e podar as pontas da palavra. As 2 primeiras iterações correm da mesma forma que foi observada no primeiro exemplo: podamos as pontas e , restando a palavra . A vida pregou-nos uma partida, e a palavra tem comprimento ímpar. Contudo, fomos inteligentes, e já mais atrás tínhamos notado e criado transições auxiliares para esta situação! Procurando seguir os estados associados a este processamento, partimos de , seguindo para (estamos a ler ) e movendo o cursor para a direita.Lemos a palavra vazia, pelo que mudamos o cursor para a esquerda e trocamos de estado para . Aqui, tendo a tal transição auxiliar, podemos aceitar a palavra (já que, movendo-nos para a esquerda, apenas encontrámos mais um ), sendo a palavra assim aceite.
Variantes
Há na literatura bastantes variações sobre a definição de máquina de Turing. Analisamos de seguida algumas, que nos serão úteis. Apesar de permitirem maior flexibilidade aparente, na verdade os modelos que analisaremos são essencialmente equivalentes ao modelo original, do ponto de vista da teoria da computabilidade.
Máquinas com transições-
Uma máquina com transições- é uma máquina cuja função de transição tem como contradomínio , em vez de . Este último elemento corresponde a um movimento em que a cabeça de leitura/escrita não muda de sítio.
As noções introduzidas na secção anterior são facilmente estendíveis a estas máquinas, sendo relevante apenas realçar a extensão da função de transição de configurações, que agora, além do apresentado acima, satisfaz ainda:
Toda a máquina de Turing com transições- é equivalente a uma máquina de Turing tradicional.
Prova
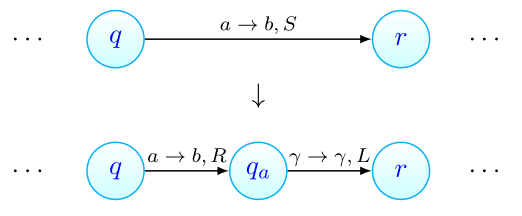
Converter uma máquina com transições- numa máquina de Turing é razoavelmente simples. Basta pegar em cada movimento e desdobrá-lo em dois movimentos, como apresentado em baixo:
em que denota um novo estado da máquina, e deve ser expandido para representar todas as letras do alfabeto .
É fácil de verificar que os dois segmentos acima levam à mesma transição de configurações.
Máquinas bidirecionais
Uma máquina bidirecional é como uma máquina de Turing, onde se assume que a fita é infinita em ambas as direções.
Mais uma vez, a única diferença assinalável é na função de transição de configurações, que é agora definida de forma que:
Devem-se entender as transições acima como "se não houver nada à esquerda e andarmos para a esquerda, vamos para uma célula vazia".
Por contraste, as máquinas de Turing introduzidas inicialmente dizem-se unidirecionais.
Toda a máquina de Turing bidireccional é equivalente a uma máquina de Turing unidirecional.
Prova
Note-se que mover uma palavra para a direita numa fita unidirecional é algo relativamente fácil.
Para uma dada computação numa máquina bidirecional, delineamos a computação respetiva numa máquina de Turing unidirecional da seguinte forma:
Sempre que a computação da fita bidirecional determinar que é preciso um espaço à esquerda da palavra, movemos toda a palavra para a direita.
Desta forma, criamos um espaço na primeira posição onde podemos colocar o símbolo determinado pela computação da fita bidirecional.
Uma forma de saber quando precisamos de um espaço à esquerda é, antes da computação, movermos o input um espaço para a direita.
Assim, sempre que lermos um espaço em branco depois de fazermos um movimento para a esquerda, quer dizer que precisamos de mais um espaço à esquerda.
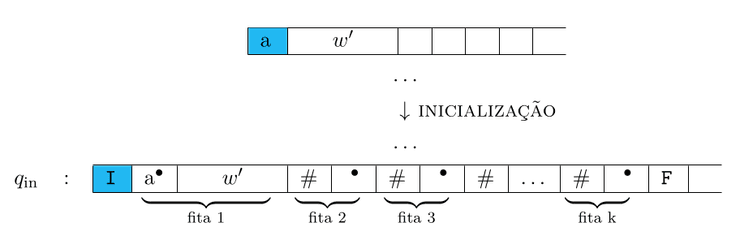
Máquina multifita
Definimos uma máquina de Turing multifita como uma máquina de Turing cuja função de transição é (para algum ) do tipo
Para uma máquina de Turing multifita, convenciona-se que o input é sempre colocado na primeira fita, e o output é sempre devolvido na última fita.
Toda a máquina de Turing multifita é equivalente a uma máquina de Turing com apenas uma fita.
Prova
Intuitivamente, se conseguirmos dividir a fita da máquina de Turing em secções "independentes", conseguimos arranjar uma equivalência entre a máquina de Turing tradicional. Precisamos no entanto de:
- um símbolo para separar as diferentes secções da fita (que correspondem às várias fitas da máquina multifita) - vamos usar o símbolo ;
- símbolos para demarcar o início e fim da fita - vamos usar e ;
- símbolos idênticos aos do nosso alfabeto de trabalho, mas que assinalem que a cabeça de escrita/leitura da respetiva fita está nessa posição - vamos chamar a este conjunto .
Vamos então usar o alfabeto .
Vamos então tentar construir uma máquina de Turing tradicional que compute o mesmo que uma máquina multifita .
A máquina começa por criar uma fita da seguinte forma: - coloca na primeira posição;
- coloca na segunda posição a correspondente em ao primeiro símbolo no input de ;
- coloca na fita a seguido de uma vez por cada fita de ( vezes);
- acaba por colocar o símbolo de terminação .
Com a fita de inicializada, podemos agora fazer as mudanças indicadas por .
Isto é feito da seguinte forma: da esquerda para a direita, reconhecemos onde está a cabeça de escrita/leitura das correspondentes a cada uma das fitas, e fazemos a alteração necessária.
Note-se que poderá ser necessário mover símbolos para a direita para disponibilizar novos espaços para alguma fita.
É importante realçar que, no final, de forma a que devolva o mesmo output que , temos de converter o símbolo de do espaço correspondente à última fita no correspondente símbolo de , bem como remover o no final da fita.
Máquinas não-deterministas
Uma máquina de Turing não-determinista é como uma máquia de Turing tal que a função de transição é do tipo
Tal como com os autómatos, dizemos que uma máquina de Turing não-determinista aceita uma palavra se existir uma computação que aceite a palavra, dizendo-se que rejeita a palavra se todas as computações forem finitas e rejeitarem a palavra. Note-se que uma máquina de Turing pode ter computações que entram em ciclos e portanto são infinitas.
Toda a máquina de Turing não-determinista é equivalente a uma máquina de Turing determinista.
Prova
Vamos, mais uma vez, definir para uma máquina não-determinística , definir uma máquina de Turing que lhe seja equivalente.
A ideia será que terá 3 fitas:
- a primeira fita manterá o input do problema, sem o alterar;
- a segunda fita será usada para escolher o caminho a percorrer no grafo das possíveis transições de configurações;
- a terceira fita será usada para mexer no input para cada sequência na fita 2.
A máquina começa por inicializar as fitas:
- na segunda fita coloca $ para indicar o início do caminho, abre (depende do input) espaços vazios, e coloca no final para indicar o fim do caminho.
- copia-se para a terceira fita o input.
Então, executamos na fita 3 de acordo com o caminho 2 até que:
- cheguemos a um estado de aceitação de : neste caso vamos para o estado de aceitação de e terminamos a computação;
- cheguemos a um estado de rejeição de : neste caso passamos ao próximo caminho na fita 2.
Se nenhum dos caminhos na fita 2 aceitar a palavra, então a palavra deve ser rejeitada.
Máquina Universal
Podemos verificar que o alfabeto é suficiente para representar qualquer problema.
Por exemplo, como é amplamente sabido, a representação em base 10 dos números pode ser substituída por uma representação binária.
Há na verdade várias representações em base binária para os números naturais.
Se fizermos por exemplo a correspondência entre cada algarismo para uma palavra binária, obtemos uma representação binária diferente da tradicional.
Mais genericamente, é possível definir uma tradução para binário semelhante à explicada a cima para qualquer alfabeto.
Mais ainda, é possível definir uma representação binária para uma Máquina de Turing.
Abaixo vemos os detalhes destas representações, tanto de uma representação de um alfabeto em binário como uma representação para Máquinas de Turing, a que damos o nome de representação canónica.
Representação Canónica
Para uma máquina de Turing , a representação canónica é uma string da forma:
que pode ser descrita da seguinte forma:
-
uma string de 1's: tantos quanto o número de estados na máquina de Turing, isto é, tantos quanto os estados em : os estados são identificados da seguinte forma:
-
um 0 de separação;
-
uma string de 1's: tantos quantos símbolos no alfabeto auxiliar : os símbolos são da seguinte forma:
-
um 0 de separação;
-
uma sequência de strings que representam as transições dadas pela função : cada string que representa uma transição é uma palavra de comprimento .
Assim, estamos capacitados de confundir uma máquina de Turing com uma palavra binária, quando apropriado. Desta forma, podemos falar em linguagens que incluam certas Máquinas de Turing, que será aquilo em que estaremos interessados.
Exemplo de Representação Canónica
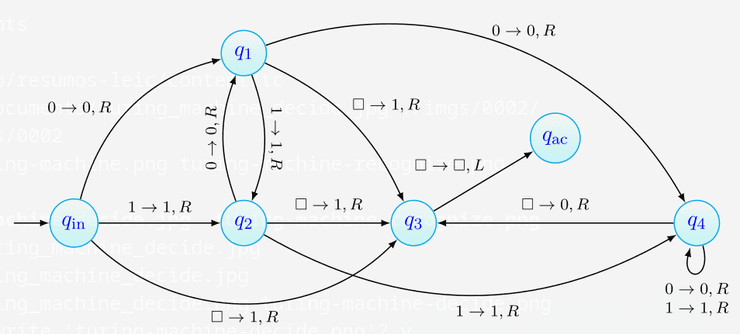
Consideremos por exemplo a seguinte máquina de Turing, que decide a linguagem das palavras sobre que começam com dois 's consecutivos:
A sua representação canónica é:
A máquina tem estados (, , e ).
O alfabeto de trabalho da máquina tem símbolos: , e .
A máquina tem duas transições, representadas acima.
Dado um alfabeto , denotamos por o conjunto das representações canónicas de máquinas de Turing com alfabeto de entrada/saída .
Denotamos por a representação canónica de uma palavra .
Por exemplo, para temos que , , e por aí a diante.
Vamos então chegar à proposição que motiva todas estas representações.
Proposição
Existe uma máquina de Turing , a que damos o nome de máquina Universal, que para qualquer e , tal que, para um símbolo
- U aceita (respetivamente rejeita) se e só se aceita (resp. rejeita) ;
- .
Prova
Seja uma máquina de Turing com 6 fitas.
A máquina, ao receber um input , começa por verificar se a palavra é da forma para alguma máquina de Turing e , rejeitando se este não for o caso.
Passada esta verificação, a máquina passa para a fase inicial:
- copia a sequência de 's correspondente ao número de estados de para a fita 2;
- copia a sequência de 's correspondente ao número de símbolos de para a fita 3;
- copia as transições de para a fita 4;
- coloca o estado inicial de na fita 5;
- copia para a fita 6;
- coloca as cabeças de leitura/escrita de cada fita no início destas palavras.
Após a fase inicial, a máquina entra na fase de simulação. Nesta fase, faz os seguintes passos repetidamente até abortar/terminar.
- lê o símbolo onde está posicionado a cabeça de leitura/escrita da fita 6;
- lê o estado atual de na fita 5;
- percorre a fita 3 à procura da transição de para este símbolo e estado. Se não encontrar transição, aborta. Se encontrar, altera o estado de na fita 5, o símbolo na fita 6 e a posição da cabeça de leitura/escrita conforme indicado na transição encontrada;
- Se o passo anterior levar a um estado de terminação de , termina em concordância com .
A existência desta máquina permite-nos falar por exemplo "na linguagem de palavras da forma tal que a máquina de Turing aceita ". Isto vai ser bastante relevante no próximo capítulo.