Algoritmos Elementares sobre Grafos
Vamos procurar rever e aprofundar conceitos previamente abordados em IAED, tais como DFS (incluindo ordenação topológica e componentes fortemente ligados) e BFS.
DFS - Depth First Search
Consiste num algoritmo recursivo que utiliza a noção de backtracking. Procura esgotar todos os caminhos possíveis em frente, voltando para trás quando já não há mais possibilidades de seguir em frente.
Exemplo simples da execução do algoritmo
Consideremos o seguinte grafo:
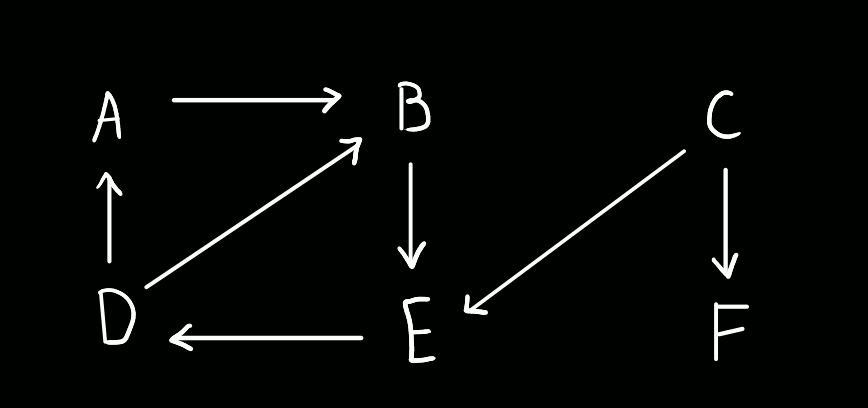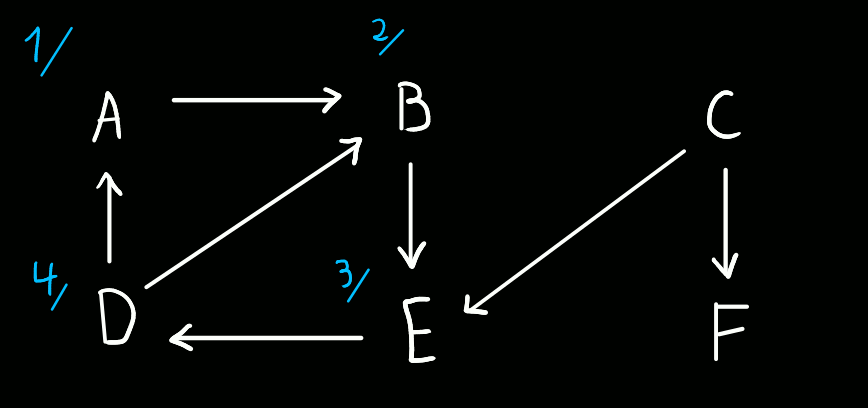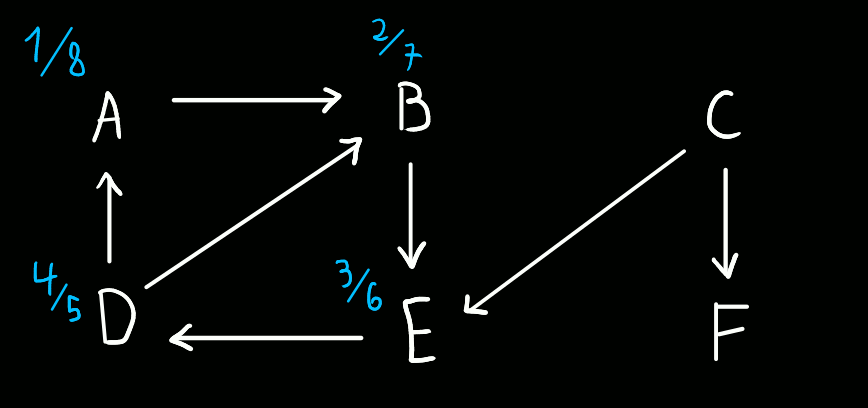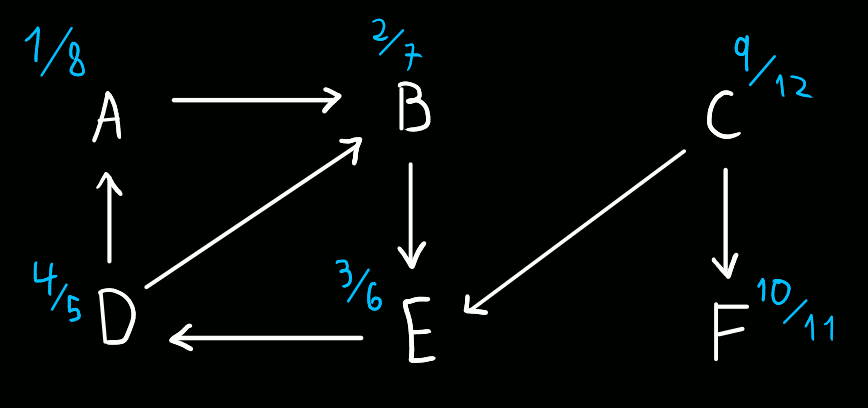
Tenhamos ainda que, em caso de empate entre dois vértices, o algoritmo deve escolher o vértice que vem antes por ordem alfabética. Começaremos no vértice A.
-
Do vértice A, podemos ir apenas para o vértice B. (timestamp 1 a "abrir" A)
-
Do vértice B, podemos ir apenas para o vértice E. (timestamp 2 a "abrir" B)
-
Do vértice E, podemos ir apenas para o vértice D. (timestamp 3 a "abrir" E)
-
Do vértice D, podemos ir para os vértices A e B. Contudo, ambos já foram visitados, pelo que não temos para onde ir, e assim que descobrimos D, trancamo-lo. (timestamp 4 a "abrir" D, timestamp 5 a "fechar" D)
(começa aqui um backtracking, após o "fecho" de um vértice)
-
Do vértice E não temos para onde ir, pelo que o trancamos. (timestamp 6 a "fechar" E)
-
Do vértice B não temos para onde ir, pelo que o trancamos. (timestamp 7 a "fechar" B)
-
Do vértice A não temos para onde ir, pelo que o trancamos. (timestamp 8 a "fechar" A)
Trancámos, então, o vértice onde começámos a procurar - restam, contudo, vértices por explorar. Assim sendo, começamos uma nova procura, desta vez pelo vértice C.
-
Do vértice C, podemos ir apenas para os vértices E e F. Contudo, E já foi visitado, pelo que optamos por ir para F. (timestamp 9 a "abrir" C)
-
Do vértice F não temos para onde ir, pelo que o trancamos. (timestamp 10 a "abrir" F, timestamp 11 a "fechar" F)
-
Do vértice C não temos para onde ir, pelo que o trancamos. (timestamp 12 a "fechar" C)
Aqui, terminamos a procura - não restam vértices por explorar.
A tabela abaixo indica os tempos de descoberta e fecho de cada vértice:
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 2 | 9 | 4 | 3 | 10 | |
| 8 | 7 | 12 | 5 | 6 | 11 |
(Aqui, corresponde ao tempo de descoberta e ao tempo de fecho)
Ao resolver um exercício de procura DFS, provavelmente optar-se-ia por desenhar algo deste género:
Podíamos ainda, no fim, desenhar a floresta DFS do grafo acima. O conceito será abordado mais abaixo.
No algoritmo que estudámos em aula, cada vértice do grafo tem algumas propriedades que facilitam o desenrolar da DFS:
-
cada vértice tem um pai,
pi, inicialmente nulo (Nil, no pseudocódigo), que corresponde ao seu predecessor na procura. -
cada vértice tem uma cor -
White,GrayouBlack. Um vértice éWhiteantes de ser descoberto,Grayentre descoberta e fecho, eBlackquando está fechado. -
cada vértice tem um tempo de descoberta e um tempo de fecho.
Tendo como argumento um grafo , o pseudocódigo do algoritmo da DFS pode ser tal que:
// every graph G has a set of vertices V
DFS(G)
for v in G.V // loop 1
v.color = White
v.discovery = 0
v.closure = 0
v.pi = Nil
time := 0
for v in G.V // loop 2
if v.color == White
DFS_Visit(G, v)
DFS_Visit(G, v)
time = time + 1
v.discovery = time
v.color = Gray
for w in G.Adj[v] // loop 3
if w.color == White
w.pi = v
DFS_Visit(G, w)
time = time + 1
v.closure = time
v.color = BlackAs complexidades temporais (agregadas - durante todo o decorrer do algoritmo) de cada loop acima são:
- Loop 1 -
- Loop 2 -
- Loop 3 -
Onde é o número de vértices do grafo e o número de arcos/arestas.
A complexidade do primeiro loop é trivial, o loop é claramente executado apenas uma
vez para cada vértice. A do segundo também segue a mesma lógica, sendo executado uma
vez para cada vértice. A do terceiro não é óbvia. Temos cada, para cada vértice,
DFS_Visit é chamada apenas uma vez (porque assim que deixa o estado White, não
volta a poder ter esse estado). Além disso, para cada vértice, o loop é executado
vezes, uma vez para cada arco/aresta que liga aquele vértice a outro. Isto,
claro, considerando todo o decorrer do algoritmo - foi assim que a complexidade do algoritmo foi abordada em aula.
Resta ainda realçar que foi utilizado e não - os loops, aqui, são executados exatamente com aquela complexidade, sempre, qualquer que seja o grafo-argumento do algoritmo.
A complexidade temporal total do algoritmo é, portanto, .
Floresta DFS
Uma árvore DFS corresponde à representação de uma procura DFS pela ordem em que os vértices são descobertos. A raiz da árvore é o vértice inicial. Um vértice pode ter mais do que um filho, caso haja mais que um vértice a ser descoberto a partir dele, mas apenas um pai. O conjunto de árvores DFS de um grafo diz-se uma floresta DFS.
Pode existir mais que uma floresta DFS possível num grafo.
Temos, abaixo, dois exemplos de grafos com respetivas florestas DFS:
Exemplo 1 - Floresta com uma árvore
Exemplo 2 - Floresta com mais do que uma árvore
Exemplo 3 - Variação do exemplo anterior
Podemos, ainda demonstrar que há mais do que uma floresta possível para um dado grafo. Pegando no grafo do exemplo anterior, e fazendo uma DFS diferente (começando, por exemplo, em C):
Podemos, na floresta DFS, representar vários tipos de arcos (arcos estes que representam arcos do próprio grafo):
-
Tree edges - as arestas "normais" da árvore, consecutivas, de nó em nó.
-
Forward edges - arestas "para a frente", não consecutivas.
-
Back edges - arestas "para trás", não consecutivas.
-
Cross edges - arestas "cruzadas". Ao contrário das outras arestas, estas não correspondem a descendentes/ascendentes diretos - podemos pensar nelas como relações entre primos, tios, etc.
Exemplo - Tipos de Edges
Pegando no grafo do Exemplo 1 acima:
Nem todas as arestas do grafo estão representadas nesta árvore DFS - estão apenas representadas as arestas "normais" da árvore - tree edges. As restantes arestas são, respetivamente (olhando para o grafo original):
- - Forward edge
- - Back edge
- - Back edge
- - Cross edge
- - Cross edge
Poderiam ser representadas tal que:
Em termos de tempos de descoberta, para cada tipo de aresta, temos que (tendo dois vértices, e ):
-
temos um tree ou um forward edge de para caso .
-
temos um back edge de para caso .
-
temos um cross edge de para caso .
Antes de abordar a ordenação topológica e os componentes fortemente ligados, é relevante enunciar o Teorema do Caminho Branco.
Teorema do Caminho Branco
Tendo dois vértices e , temos que é descendente de se e apenas se, no momento em que é descoberto, existir um caminho de vértices brancos - por descobrir - a ligar a .
Podemos, ainda, provar que um grafo tem um caminho circular se e apenas se a DFS revela um arco para trás. A prova encontra-se abaixo.
Prova do Lema acima
Vamos ter, portanto, de procurar provar a equivalência apresentada. Provar a implicação da direita para a esquerda é fácil - temos que uma back edge só existe entre parentes diretos, pelo que se esta existir uma back edge , então podemos começar um caminho que parte de , chega a e volta a , estando, portanto, na presença de um ciclo. A parte complicada reside em provar a implicação da esquerda para a direita - se um grafo tem um caminho circular, então a DFS revela uma back edge.
Tenhamos um qualquer caminho circular do tipo . Podemos procurar ordená-lo por ordem crescente de tempo de descoberta - ficaríamos com um caminho . Temos, pelo teorema do caminho branco, que são todos descendentes de na floresta DFS - assim sendo, é necessariamente uma back edge.
Ordenação Topológica
Ordenação Topológica
Sequência que contém todos os vértices de um grafo apenas uma vez, tal que se , então aparece antes de na ordem topológica. Devido a esta última propriedade, só podemos realizar ordenações topológicas em grafos acíclicos.
Segundo o professor, para resolver exercícios associados a ordenação topológica, pode dar jeito desenhar o grafo na horizontal, como pode ser observado abaixo:
Podemos, aqui, admitir que uma ordenação topológica possível (não a única) é , já que ao escrever os arcos do grafo, estes apontam todos para a frente:
Lema
Se é um DAG (grafo acíclico dirigido) e , então é fechado antes de .
-
Caso , então , logo é fechado antes de .
-
Caso contrário, então *, logo é fechado antes de .
* podemos afirmá-lo já que, caso contrário, poder-se ia descobrir primeiro e depois , antes de se fechar . Como há um arco de para , teríamos encontrado um ciclo - o grafo, contudo, é um DAG, acíclico por definição - impossível de acontecer.
Uma ordenação topológica pode, então, ser dada pela ordem decrescente de tempos de fecho de uma DFS a um dado grafo. Por exemplo, dado o grafo abaixo e respetiva DFS a começar em :
A ordenação topológica via ordem decrescente de tempos de fecho é dada por . Podemos, claro, confirmar que não há back edges (para confirmar que a ordenação topológica está feita corretamente):
SCCs - Componentes Fortemente Ligados
SCC
Dado um grafo , um conjunto de vértices diz-se um SCC, componente fortemente ligado, de se e apenas se:
-
(por esta última parte entenda-se "há um caminho de para e um de para "). Colocando em termos mais simples, escolhendo um vértice qualquer do SCC, podemos criar um caminho que chegue a todos os outros vértices do mesmo SCC.
-
É maximal, isto é, não está contido em nenhum outro SCC - não existe um tal que é um subconjunto seu.
Por exemplo, dado o grafo abaixo:
Temos dois SCCs - e . não pertence a porque, apesar de ser possível construir um caminho de para , o contrário não se verifica.
Podemos desenhar um grafo dos componentes.
Grafo dos Componentes
Seja um grafo dirigido. O grafo dos componentes de é dado por , onde:
-
é o conjunto dos SCCs de .
-
é o conjunto de todas as arestas de que ligam um SCC a outro. Colocando a afirmação de forma mais formal, temos De realçar que pode haver mais que uma aresta a ligar dois componentes.
O tempo de descoberta de um componente corresponde ao tempo de descoberta do vértice que lhe pertence que é descoberto primeiro. O tempo de fecho de um componente corresponde ao tempo de fecho do vértice que lhe pertence que é fechado por último.
Os componentes de um grafo e os do seu grafo transposto (com todos os arcos no sentido contrário) são necessariamente iguais.
Exemplo - Grafo dos Componentes
Dado o grafo abaixo:
O grafo dos componentes correspondente é dado por:
Os grafos dos componentes gozam de um par de propriedades interessantes.
A primeira diz-nos que, dados dois vértices e de , se pertence a um SCC e pertence a um outro SCC , e existe uma aresta , então não pode existir qualquer aresta tal que - caso contrário, nenhum dos componentes seria maximal, já que poderíamos fazer caminhos entre todos os vértices de ambos os componentes em questão. Esta propriedade permite-nos, ainda, afirmar que o grafo dos componentes é um DAG, necessariamente.
A segunda diz-nos que, tendo dois SCCs, e , se temos uma aresta que vai de um qualquer vértice de para um qualquer vértice de , então obrigatoriamente . A prova encontra-se abaixo.
Prova da segunda propriedade - Grafo dos Componentes
Temos 2 casos em que precisamos de nos focar: e .
-
No primeiro caso, descobrimos antes de . Seja o primeiro vértice de a ser descoberto. No momento em que é descoberto, existe necessariamente (porque temos um caminho de para ) um caminho de vértices brancos a ligar a todos os vértices de . Assim sendo, concluímos, pelo Teorema do Caminho Branco, que todos os vértices de são, nesta DFS, descendentes de , pelo que o tempo de fecho de é necessariamente menor que o tempo de fecho de e, por consequência, que o tempo de fecho de .
-
No segundo caso, descobrimos antes de . Como, pela propriedade 1, não podemos ter um caminho de para , podemos garantir que o tempo de fecho de é anterior ao tempo de descoberta de e, por consequência, anterior ao tempo de fecho de .
A propriedade 2 fica, então, provada.
O algoritmo para chegar aos SCCs de um grafo é bastante simples:
- Fazer uma DFS normal, guardando uma lista com os vértices ordenada de modo decrescente pelos respetivos tempos de fim.
- Transpor o grafo - alterar o sentido de todos os seus arcos.
- Fazer outra DFS (ao grafo transposto), seguindo desta vez a ordem decrescente que guardámos no primeiro passo. A ordem decrescente é relevante ao escolher a raiz do caminho, mas aquando da exploração do caminho em si, não importa - podemos escolher qualquer vértice.
Cada árvore da floresta DFS do grafo transposto corresponderá a um SCC do grafo original.
A complexidade temporal de ambas as DFS é . A da transposição é (considerando que a representação das arestas é feita através de uma lista de adjacências). Assim, a complexidade temporal do algoritmo como um todo será .
Exemplo da aplicação do algoritmo
Tenhamos o grafo abaixo (com DFS inicial já realizada, respetivos tempos de descoberta e de fecho indicados):
Os vértices, por ordem decrescente de tempo de fim, serão então .
O respetivo grafo transposto será o seguinte:
Por fim, a DFS realizada por ordem decrescente dos tempos de fim da DFS inicial é tal que:
Assim sendo, a floresta DFS final é:
Temos 5 árvores na floresta DFS, pelo que temos 5 SCCs. O grafo dos componentes correspondente é, então:
BFS - Breadth First Search
É, tal como a DFS, um algoritmo para travessia de grafos. Se na DFS o objetivo prendia-se em percorrer os caminhos em profundidade, até eventualmente ter de voltar para trás (backtracking), na BFS o objetivo passa por percorrer os caminhos em largura. Utiliza a noção de fila (vulgo queue) para guardar os vértices a serem explorados num futuro próximo. O próximo vértice a ser explorado é sempre o que está no início da fila. De realçar ainda que utilizamos uma fila regular, do tipo FIFO, first in first out.
Começamos na raiz, com a fila inicialmente vazia, e vamos adicionando os vértices adjacentes ao vértice atual à fila. Fazemo-lo sucessivamente, extraindo sempre o primeiro elemento da fila e repetindo o processo até a fila estar vazia - quando estiver, a procura está concluída.
O pseudocódigo do algoritmo é o seguinte:
BFS(G, v) // v é o vértice-raiz da procura
for each n in V except v
n.color = white
n.distance = inf // inicialmente a infinito
n.pi = nil
v.color = gray
v.distance = 0
v.parent = nil
Q := new queue
Q.enqueue(v)
while Q is not empty
u := Q.dequeue()
for each n in Adj(u)
if n.color == white
n.color = gray
n.distance = u.distance + 1
n.pi = u
Q.enqueue(n)
u.color = blackExemplo de Aplicação do Algoritmo
Vamos utilizar um grafo não dirigido, como o seguinte:
O decorrer do algoritmo é:
- Começamos por explorar - tem adjacências e , pelo que adicionamos esses vértices à queue.
- Exploramos , por ser o próximo vértice da queue, e adicionamos (a sua única adjacência) à queue.
- Exploramos , e adicionamos e à queue.
- Exploramos , que não tem qualquer adjacência, pelo que não se adiciona nada à queue.
- Exploramos , que tem como adjacências e . já foi adicionado à queue por , pelo que apenas é adicionado.
- Exploramos , que tem como adjacências , e . Todos exceto já foram adicionados à queue previamente, pelo que apenas é adicionado.
- Exploramos , que não tem adjacências por explorar, pelo que nada é adicionado.
- Exploramos , que não tem adjacências por explorar, pelo que nada é adicionado.
O algoritmo termina aqui. Os números ao lado de cada vértice correspondem à distância do vértice que escolhemos como raiz da BFS, neste caso o vértice . A estrutura vertical que podemos observar à esquerda corresponde à fila em que os vértices iam sendo colocados.
Em termos de complexidade (agregada), podemos dizer que o primeiro loop (for)
tem complexidade (passa por todos os vértices menos um, sem operações
recursivas no seu interior), enquanto que o segundo loop (while) tem complexidade
, já que a queue irá incluir todos os vértices, e para cada vértice
são verificadas todas as suas adjacências. Podemos, assim, admitir que a complexidade temporal da BFS é .
Árvore Breadth-First
Por árvore BF temos um sub-grafo de correspondente à travessia BFS por a começar num dado vértice . A árvore BF a começar num dado vértice é igual a uma árvore DFS a começar no mesmo vértice - os vértices atingíveis a partir de uma fonte são sempre os mesmos, os "tempos" em que descobrimos cada vértice na procura é que podem ser diferentes.
Por exemplo, para a BFS:
A árvore BF correspondente é a abaixo:
As "distâncias" (os tempos indicados na BFS) correspondem a níveis da árvore (como se pode ver acima).