Corrente e Magnetostática
Corrente Elétrica
Densidade de Corrente
Na Eletrostática estudámos que as cargas que criavam um campo estavam estáticas, ao contrário da Carga de Prova que se podia movimentar livremente.
Na Corrente Elétrica estudaremos cargas de fonte que não se encontram paradas.
Temos assim de definir o conceito de Corrente Elétrica.
- A Corrente Elétrica corresponde ao fluxo de eletrões em movimento com um fluxo definido.
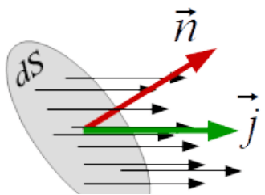
Usando o conceito matemático de fluxo podemos definir a Densidade de Corrente
A Densidade de Corrente é a quantidade de carga que passa através de um elemento de superfície perpendicular à corrente das cargas em movimento por unidade de tempo
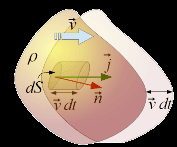
A Densidade de Corrente está relacionada com a velocidade média do fluxo das cargas.
Para uma distribuição de cargas com densidade com uma velocidade (média) , quando passam por um elemento de superfície a carga que atravessa essa superfície num intervalo de tempo é igual à cargas contida num cilindro de base e altura
Para cargas por unidade de volume temos que
Corrente Elétrica
A carga total que passa por unidade de tempo através da superfície chama-se
Corrente Elétrica e é igual ao fluxo da densidade de corrente através da superfície
- Mede-se em Ampere
- Representa a taxa a que a carga deixa um volume delimitado por uma superfície
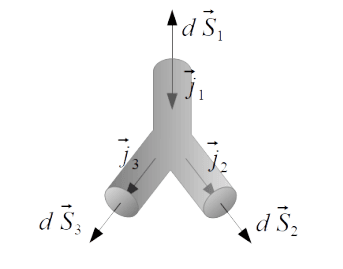
A Carga Elétrica é indestrutível, isto é, é conservada, não se pode criar nem destruir.
A Lei da Conservação da Carga é assim dada por
é uma superfície fechada.
A Lei da Conservação da Carga pode também ser escrita na forma diferencial
No caso de um fio de comprimento e secção e de corrente uniforme o elemento de volume é
Assim se o fio for muito fino temos uma densidade linear de carga
Se as cargas positivas e negativas se movimentarem no fio
Lei de Kirchhoff
Não sai no 2º Teste (2021/2022)
As Leis de Kirchhoff não serão avaliadas no segundo teste
Lei das Malhas
Esta lei é uma consequência do Campo Elétrico ser Conservativo, o trabalho (mínimo) para transportar uma carga ao longo de um circuito fechado é nulo.
Lei os Nodos
Para uma junção que não acumula nem perde energia, a carga total permanece constante nessa zona do circuito. Assim
Lei de Ohm
Para ter corrente é preciso empurrar as cargas, a velocidade que adquirem depende das características do material.
A Densidade de Corrente é proporcional à força por unidade de carga
é uma constante experimental que depende do material e chama-se Condutividade do meio.
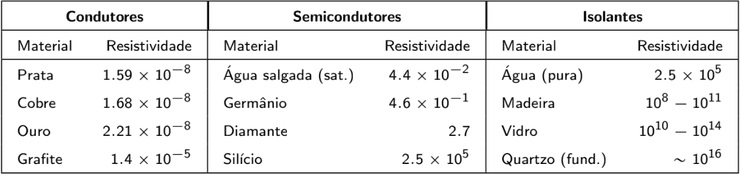
Mais familiar deverá ser o termo que é a Resistividade (Elétrica).
Os Isolantes também têm uma condutividade mas que difere na ordem de a comparar com os Condutores. Por simplificação vamos assumir que os metais são condutores perfeitos
Nesta parte da matéria assumimos que a força aplicada nas cargas é a do Campo Eletromagnético.
Para um único Campo Elétrico:
Num condutor em Equilíbrio Eletrostático temos e
Para condutores perfeitos , mesmo que esteja corrente a fluir.
Conclui-se que o campo elétrico necessário para movimentar as cargas é quase nulo.
Assim consideramos estes fios como Equipotenciais.
Já as resistências são feitos de materiais que conduzem pouco.
A Lei de Ohm é então dada por
é a Resistência, expressa-se em ohms
Quando a carga que entra num dado volume por unidade de tempo é igual à que sai, dizemos que temos uma Corrente Estacionária e a sua Densidade de Carga é constante.
Para correntes estacionárias e condutividade uniforme
Isto significa que qualquer carga não contrabalançada se situa na superfície.
A partir das equações anteriores podemos calcular as condições fronteira onde numa corrente estacionária, as cargas não se acumulam na fronteira
Lei de Joule
- Potência Emitida
Só iremos estudar correntes estacionárias que produzem campos magnéticos constantes.
Uma única carga elétrica em movimento não é uma corrente estacionária.
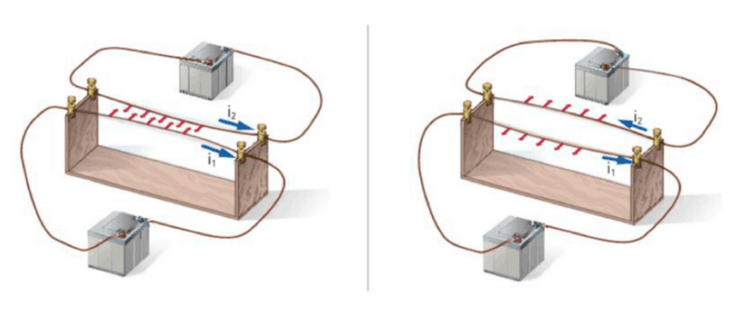
A Experiência de Ampère
Se colocarmos 2 fios condutores em paralelo com uma certa corrente podemos observar certos fenómenos:
-
Quando a corrente nos dois fios tem a mesma direção os fios atraem-se
-
Quando a corrente nos dois fios tem a direção oposta os fios repelem-se
Ampère concluiu assim que este fenómenos eram explicados pela Força Magnética.
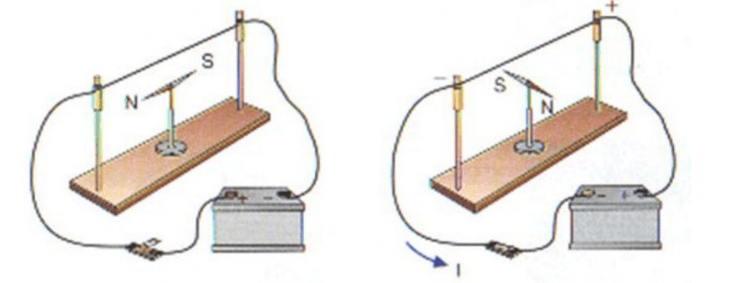
Enquanto que uma carga parada produz um Campo Elétrico , uma carga em movimento produz um Campo Elétrico e um Campo Magnético
Ørsted verificou isso usando uma bússola e vendo que esta mudava a direção perto dos fios, sobre o efeito de corrente.
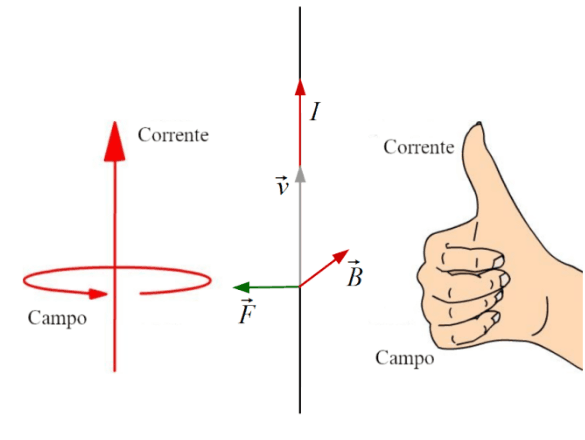
Força de Lorentz
A Força (de Lorentz) que age sobre o fio pode ser descrita como o produto externo entre a Velocidade de uma carga e um Campo Magnético que anda em círculo em torno do fio
Na presença de campos elétricos e magnéticos:
As Forças Magnéticas não produzem Trabalho.
Se a carga se mover de o trabalho é
Esta Força apenas pode mudar a trajetória de uma partícula mas nunca pode acelerá-la
Assim a Força por unidade de volume é
Para o Vetor Corrente , podemos escrever
A Força Magnética num fio depende apenas da corrente total e não depende da carga de cada partícula nem do seu sinal.
Num fio se o elemento for suficientemente pequeno temos e na mesma direção e portanto é equivalente escrever
Para constante
Sendo a corrente (vetorial) por unidade de largura perpendicular ao fluxo:
Onde é a densidade superficial de carga (móvel) e a velocidade das cargas, varia de ponto para ponto porque e podem variar.
A Força Magnética na corrente superficial é
Para uma Corrente Volumétrica
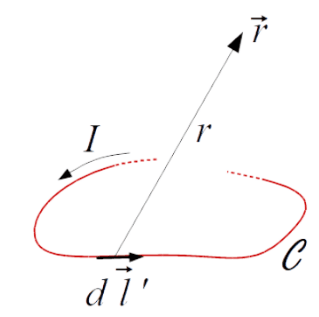
Lei de Biot-Savart
O Campo Magnético por um fio percorrido por corrente estacionária é dado por
A integração é feita segundo a direção da corrente.
é a Permeabilidade do Espaço Livre
Este número é exato e não uma constante empírica. Serve para definir o Ampere, que define o Coulomb. As unidades foram definidas de forma a que seja expresso em Newton por Ampere-metro ou Tesla (T) Usa-se mais a unidade Gausss od sistema CGS: 1 Tesla Gauss
Para temos de comparação, o Campo Magnético terrestre é igual a 0.5 Gauss. No Cern foi possível existe um íman com o valor de 3.8 Tesla
Lei de Ampère
Dedução da Lei de Ampère
Existem nos slides uma explicação de como se chegou a estas Leis
Slides: