Eletrostática e Fluxo e Introdução ao Potencial
Exercícios
No final da página encontram-se resoluções mais pormenorizadas dos exercícios feitos em aula
Eletrostática
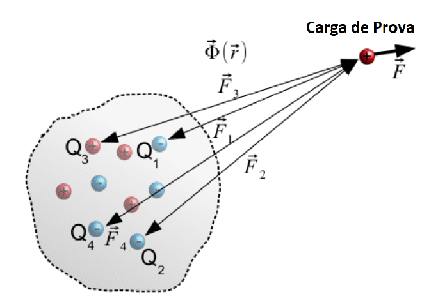
Supomos que temos uma distribuição de cargas.
Para calcularmos o valor do campo em cada ponto do espaço precisamos de uma carga de prova.
Uma carga de prova é uma carga independente do campo e que pode ser escolhida pelo leitor.
As cargas que criam o campo são as fontes do campo.
A carga de prova sofre a força criada pelas cargas que se encontram na fonte do campo.
A posição das fontes (em função do tempo) é conhecida.
Princípio da Sobreposição
A interação entre duas cargas não é afetada pela presença das outras cargas.
A força exercida numa carga é igual à soma de todas as forças exercidas nela.
Tanto as fontes como as cargas estão sempre em movimento e o campo depende da posição, da velocidade e aceleração de todas as cargas.
Além disso, o campo propaga-se à velocidade da luz ()
Eletrostática
Nesta parte da matéria assumimos que todas as fontes estão estacionárias,
no entanto a carga de prova pode se encontrar em movimento.
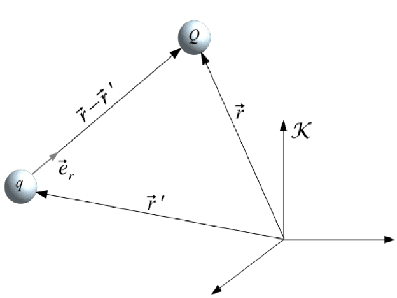
Lei de Coulomb
A força na carga de prova criada pela carga de fonte (em repouso) a uma distância é dada por
e - Cargas - unidades SI - Coulomb ()
- permitividade elétrica do espaço livre -
Sinal
Esta força só é atrativa se as cargas tiverem sinais diferentes.
Juntando a Lei de Coulomb e o Princípio da Sobreposição:
Campo Elétrico
Assim o Campo Elétrico gerado pelas fontes é:
Propriedades do Campo Elétrico (Eletrostático)
- O Campo elétrico é uma grandeza vetorial
- Depende da posição da carga de prova
- Depende da posição e da carga das fontes
- Fisicamente representa a força por unidade de carga que seria exercida na
carga de prova se fosse colocada num ponto
Fluxo
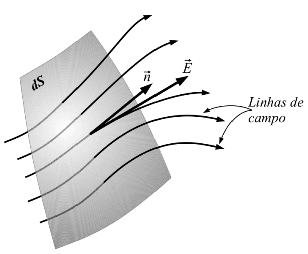
O fluxo do campo elétrico através de uma superfície é definido por:
Propriedades
- O fluxo do campo elétrico através de uma superfície "mede" o número de linhas de campo que cruzam a superfície.
- Só consideramos a componente de segundo a direção perpendicular ao elemento de superfície de .
- A intensidade do campo é proporcional à densidade das linhas de campo.
- Se o fluxo atravessa uma superfície fechada de um lado ao outro o fluxo total é nulo. No entanto, se as linhas de campo atravessam a superfície na mesma direção (sempre para fora ou sempre para dentro) há um fluxo não nulo e isso só acontece quando há cargas dentro da superfície. Esta é a essência da Lei de Gauss.
Lei de Gauss
Imaginemos que temos uma carga na origem e uma esfera de raio centrada nela.
Podemos reparar que o fluxo total não depende do raio da esfera e é proporcional à carga.
Isto é verdade para todas as superfícies fechadas e não precisa de estar centrada na carga.
Se forem cargas o Princípio da Sobreposição permite escrever e
onde é a carga contida na superfície.
Lei de Gauss (Equação Integral)
A Lei de Gauss existe porque o campo varia como
Para (densidade de carga)
Esta equação é válida para qualquer volume .
Logo o integrando tem de ser sempre nulo.
Lei de Gauss (Equação Diferencial)
Campo de uma Esfera Uniformemente Carregada
Para usar a Lei de Gauss devemos procurar usar para nossa vantagem a simetria do sistema.
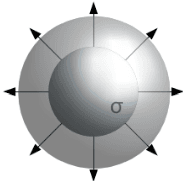
Se tivermos uma superfície esférica de raio com uma densidade superficial de carga uniforme,
como será o campo no exterior da esfera?
Imaginemos que o campo aponta para fora e para cima, se rodarmos a nossa esfera e a colocarmos de cabeça para baixo, agora esta aponta para fora e para baixo, no entanto, o campo manteve-se igual, podemos concluir assim que podemos rodar a bola como quisermos e todas essas rotações são possíveis e todas as direções em que esta aponta são válidas. Concluímos assim que o Campo criado por esta esfera é radial , segundo
Que forma de Lei de Gauss devemos usar para calcular o campo?
Através da Lei de Gauss na versão integral.
Consideremos uma superfície esférica
de raio centrada na esfera carregada.
Uma superfície desse tipo designa-se por superfície gaussiana.
Para essa superfície em cada ponto o vector unitário normal à superfície é
Assim
Como o campo tem a mesma intensidade em todos os pontos da superfície devido à simetria do sistema.
Assim pela Lei de Gauss
O campo fora da esfera é igual ao de uma carga pontual igual à da esfera centrada na origem.
Além das superfícies esféricas, as superfícies cilíndricas e superfícies planas apresentam simetrias.
Pormenores
A lei de Gauss é sempre verdade, mas nem sempre é útil. Se a densidade não fosse uniforme, ou se a superfície gaussiana não fosse uma esfera centrada na distribuição de carga, ou simplesmente se a superfície gaussiana não fosse uma esfera, a Lei de Gauss continuaria a ser verdadeira, mas isso não permitiria calcular o campo porque não poderíamos puxar para fora do integral!
A simetria é essencial para uma aplicação com sucesso da Lei de Gauss.
Para Cilindros este processo é semelhante (a sua explicação será omitida, poderão encontrar a explicação nos slides no final deste resumo)
O campo criado por um cilindro é radial perpendicularmente ao eixo do cilindro.
E provamos que
Rotacional do Campo Eletrostático
O rotacional do campo eletrostático deve ser zero.
Pelo que ficou dito sobre o potencial escalar, podemos concluir que no caminho de
Onde é uma função escalar
Slides: