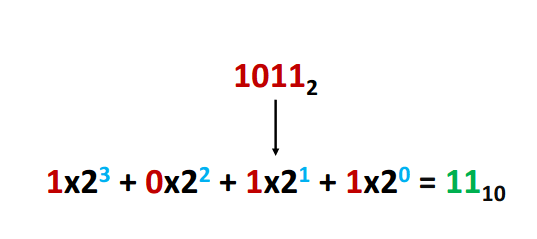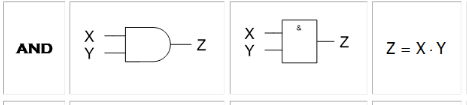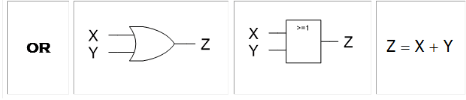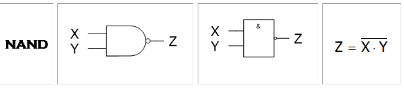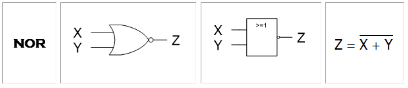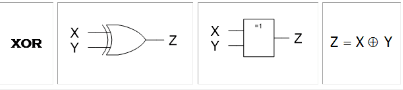Mundo binário
Bases de numeração
O ser humano faz todos os seus cálculos com base de 10, ou seja, usamos a base 10 para todas as nossas numerações, a questão que se coloca é porquê? Este vídeo explica essa razão em resposta musical.
Contudo esse facto não se mantém para os computadores e circuitos eletrónicos, pois estes usam base de 2 para fazer todos os seus cálculos, implementações e funções, visto ser mais fácil e simples de implementar esta base. Funciona por um usar um bit que pode ser o número 1 ou 0. O que torna esta base tão fácil para os circuitos eletrónicos é o facto de cada bit simbolizar algo diferente:
- Com sinal elétrico é representado por 1;
- Sem sinal elétrico é representado por 0.
Assim, os nossos computadores e dispositivos eletrónicos podem executar operações usando álgebra booleana.
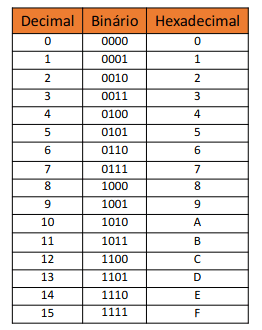
Podemos também usar qualquer outro número para representar qualquer base, usando mais ou menos símbolos. As bases atualmente mais usadas são a decimal, binária e hexadecimal, sendo que fazemos a conversão de decimal para binário para hexadecimal, como no exemplo apresentado a baixo.
Exemplo
Queremos passar o número ficamos com (em binário) e
Representação de números
Já falamos das bases em que vamos pôr os nossos números, contudo, como é que passamos de uma base para a outra sem recorrer à nossa tabela?
Começamos por ver como passar de base decimal para binário. Resumidamente só temos que ir dividindo o número por 2 continuamente e metendo o seu resto no nosso número, como no exemplo abaixo.
Exemplo
Se queremos passar o número 156 para base 2.
resto 0
resto 0
resto 1
resto 1
resto 1
resto 0
resto 0
resto 1
Ou seja ficamos com o número
Para passarmos de binário para decimal vamos apenas multiplicando o algarismo em que estamos por seja i a sua posição correspondente no número que estamos a avaliar, e i começa em 0.
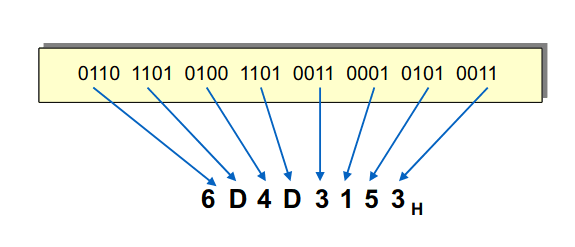
Para passarmos de um número de binário para hexadecimal temos que dividir em conjuntos de 4 algarismos o nosso número e escrever o seu número correspondente em base hexadecimal, ou seja:
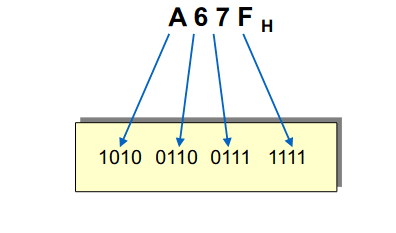
Por último passar de hexadecimal para binário é apenas fazer o inverso, isto é, a cada algarismo que temos, escrevemos os quatro algarismos correspondentes em binário:
Gama de números
Existe uma quantidade certa de números para os quais podemos representar com um determinado número de bits. Por exemplo, se queremos representar um número com N bit so podemos representar os números inteiros ou .
As duas representações diferentes ajuda-nos para o caso de termos números com ou sem sinal.
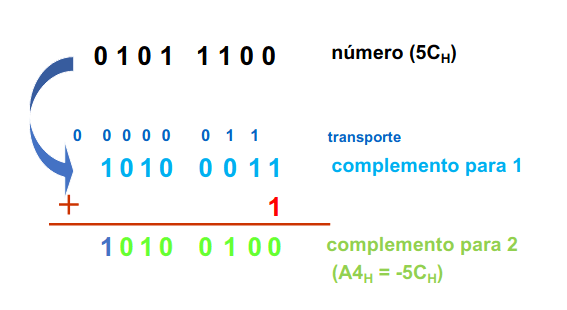
Simétrico em complemento para 2
Para obtermos o simétrico em complemento para 2 temos de inverter o valor de cada bit e no final somar 1 ao nosso número e a resposta será o nosso simétrico, como podemos observar no exemplo.
Operações lógicas
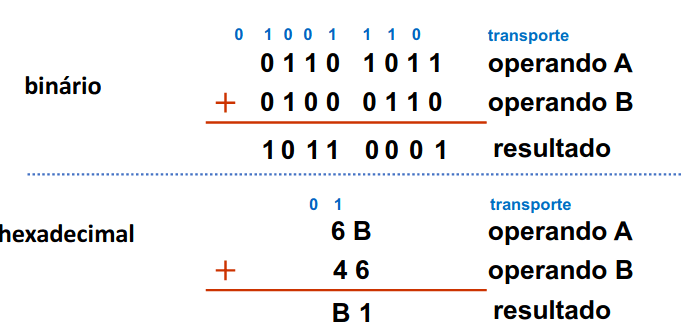
Somar dois números em binário é bastante simples, temos apenas que somar cada algarismo e se estivermos a somar dois 1s então temos que fazer "transporte" do nosso 1 para o algarismo seguinte, tendo sempre em atenção que se houver um nono bit, este será ignorado. O mesmo é feito em hexadecimal mas as nossas contas podem ir até 15 (F), sendo que a partir do 16 temos que fazer transporte de 1, 2, etc.
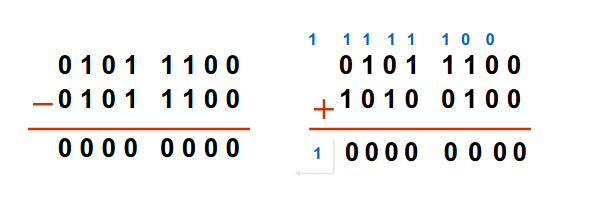
Para a subtração, temos à mesma que fazer uma soma mas fazemos o simétrico em complemento para 2 do nosso segundo número.
Excesso (overflow)
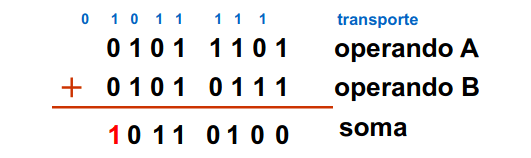
Temos que ter em atenção pois há vezes em que quando estamos a fazer algum cálculo com números em binário podemos passar de um número positivo para um número negativo ao somar dois positivos por exemplo. Isto é, no nosso resultado temos um 1 no bit mais significativo que não devia lá estar.
A solução é bastante simples! Temos apenas que aumentar o nosso número de bits! A deteção de um overflow pode ocorrer se os sinais de ambos os operandos for igual mas o resultado tem sinal diferente, visto que se ambos os operandos tiverem um sinal diferente, nunca ocorre este erro.
Portas lógicas
As portas lógicas são os circuitos que permitem executar as operações básicas de álgebra booleana. Para vermos quais são os valores de saída para cada uma das combinações dos sinais à entrada temos que usar uma tabela de verdade.
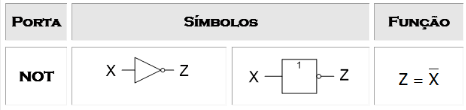
Portas NOT
As portas NOT apenas negam os nossos valores. A sua tabela de verdade é a seguinte:
| X | Y |
|---|---|
| 0 | 1 |
| 1 | 0 |
Ou seja, passamos de um valor de bit para outro.
Portas AND
As portas AND fazem uma comparação entre os dois valores fazendo uma comparação de "OU" em lógica, ou seja será representada da seguinte forma:
| X | Y | AND |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Portas OR
| X | Y | OR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Portas NAND
Resumidamente, invertem só os valores das portas AND.
| X | Y | NAND |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Portas NOR
Resumidamente, invertem só os valores das portas OR.
| X | Y | NOR |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Portas xOR
Resumidamente, se os valores forem iguais, o final será 0, mas se os valores forem diferentes, o final será 1.
| X | Y | XOR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Circuitos combinatórios
Um circuito combinatório representa um circuito digital sem re-alimentação, isto é, um circuito em que nenhuma entrada lógica depende de nenhuma saída lógica. Para a mesma combinação de valores das variáveis de entrada, os valores de saída serão sempre os mesmos, independentemente da evolução passada dos sinais de entrada. Podemos assim dizer que o circuito não tem estado interno.
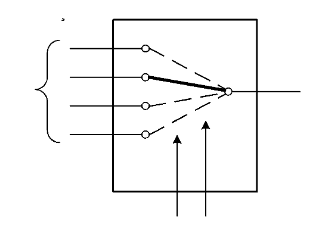
Multiplexer
Os multiplexers são circuitos que permitem escolher entre uma das várias entradas e transportar o ser valor para uma das saídas da seguinte forma:
Podemos desta forma ter multiplexers, com várias entradas e só uma saída, como por exemplo:
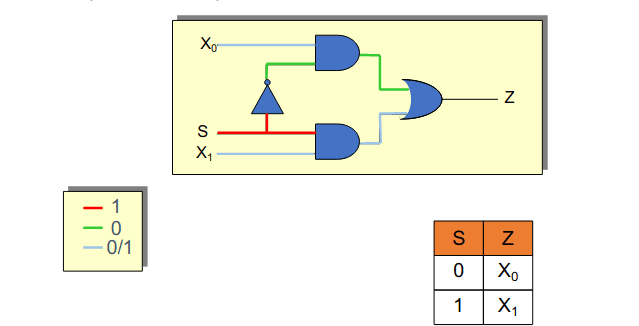
Multiplexer de 2 para 1
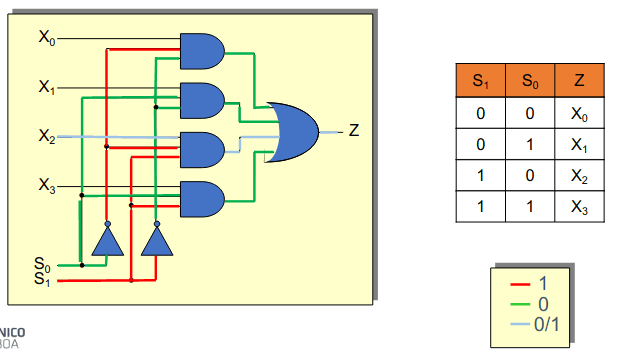
Multiplexer de 4 para 1
Circuitos sequenciais
Por outro lado, podemos ter circuitos sequenciais que são circuitos digitais com realimentação. Nestes circuitos os valores das saídas dependem não só das entradas mas também dos valores anteriores das saídas. Podemos por isso dizer que estes circuitos têm estado, isto é, têm uma combinação do valor das saídas do circuito.
Trinco (latch)
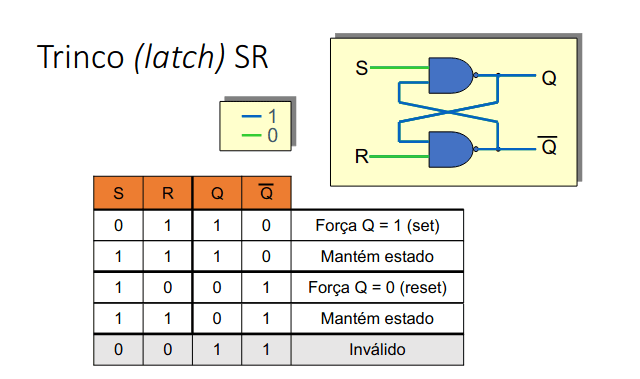
Um trinco SR é um exemplo destes circuitos sendo representado da seguinte forma:
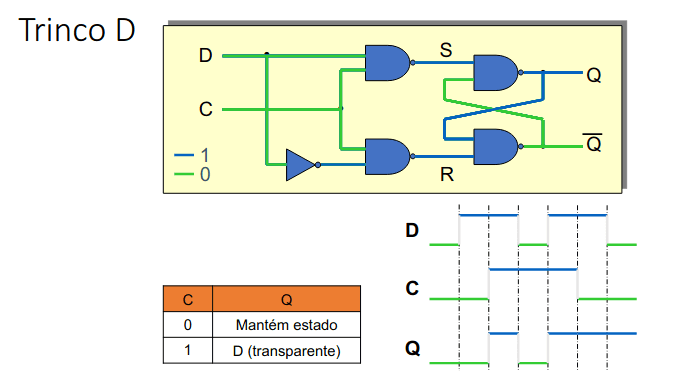
Também podemos ter trincos D que são do género:
Resumidamente, estes trincos dependem do passado e do valor atual nos circuitos. Estes circuitos sequenciais assíncronos, isto é, circuitos constituídos por portas lógicas capazes de armazenar um bit de informação, podem ou não ter variáveis de controlo.
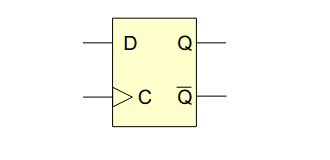
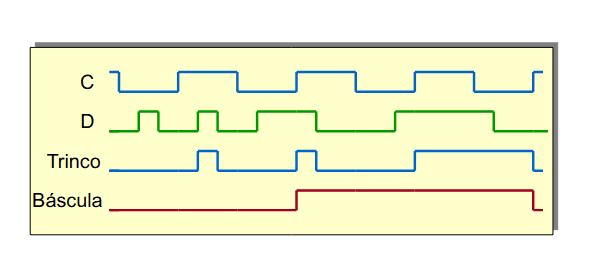
Báscula (flip-flop) D
A importância de uma báscula é memorizar o valor de D quando C transita de 0 para 1 (flanco ascendente). A principal diferença relativamente ao trinco é que a báscula mantém o valor de D mesmo que este mude, e só memoriza o valor quando C volta a transitar, portanto é na transição do sinal C que se memoriza o valor de D.
Para facilitar o pensamento, pode-se ver C como um relógio ("clock") do sistema.