Primeiro Computador
Estrutura de um computador
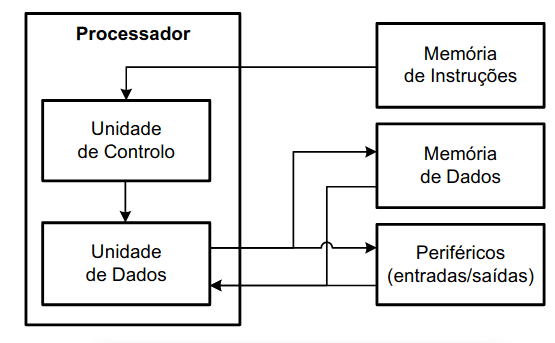
Como já é sabido, um computador é composto por muitas partes diferentes, havendo várias componentes umas ligadas às outras que trabalham independentemente ou em conjunto para que tenhamos os nossos dispositivos eletrónicos a funcionarem. Mas quais são estes componentes?
Como podemos ver pelo esquema acima, existem várias componentes num computador atual, componentes que vamos falar e aprender em maior detalhe.
Começamos por falar sobre o processador e a memória. Um processador serve para controlar tudo dentro de um computador, daí ser composto por uma unidade de controlo e uma unidade de dados. Dentro da unidade de controlo podemos observar a memória de instruções que, tal como o nome indica, avalia as instruções do programa que estamos a correr, isto é, as regras que têm que ser cumpridas. Por outro lado, dentro da unidade de dados, conseguimos observar a memória de dados e periféricos (entradas/saídas); a memória de dados avalia os dados que vamos processar, enquanto os periféricos avaliam a entrada e a saída dos mesmos, por outras palavras, funcionam como uma espécie de células de memória cujos bits ligam ao mundo exterior.
Memória de dados
Para um computador funcionar decentemente, obviamente temos que ter uma memória que vai guardando todos os dados que tanto vamos fornecendo como que vamos obtendo dos nossos programas. A memória pode ser de dois tipos:
-
RAM, Random Access Memory, que representa uma memória volátil, visto que todo o seu conteúdo é perdido quando a alimentação da memória é desligada. O seu nome provém do facto que a sua capacidade de acesso a qualquer posição e em qualquer momento é sempre aleatória.
-
ROM, Read-only Memory, que representa uma memória persistente, visto que este tipo de memória permite apenas a leitura implicando que todas as suas informações sejam gravadas pelo fabricante uma única vez e nunca podem ser alteradas ou apagadas, só podem ser acedidas.
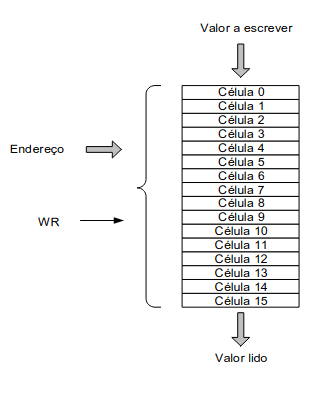
Acima, conseguimos ver um esquema de como atualmente se encontra compartimentada a memória em computadores. O objetivo destas tabelas de acesso é termos um determinado número de células com um certo tamanho. Por exemplo, se temos 4 bits para guardar a nossa informação, vamos ter 16 células, isto e células. A memória também é composta por diferentes componentes:
- Largura: representa o número de bits de cada célula ou registo;
- Tamanho: indica-nos o número de células existentes (N);
- Capacidade (bytes): é a largura x tamanho;
- Endereço: número da célula acedida, que vai de 0 ate N-1;
- WR (write): indica se o nosso acesso é de escrita ou leitura. Se estiver a 1 (ou seja está ativo), então significa que estamos a escrever na célula de memória.
Exemplo
Se estivermos perante uma tabela de endereços de memória e quisermos escrever na nona célula, como é que podemos codificar esta informação de forma a que o nosso computador perceba o que tem que ser feito?
1001 0Os primeiros 4 algarismos representam o número da nossa célula de memória, neste caso como queremos alterar os dados na célula 9, temos 1001. O último algarismo representa o bit que nos indica se estamos a ler ou escrever na célula, como está a zero, estamos apenas a ler.
Processador: unidade de dados
Temos como objetivo processar um algoritmo da soma, ou seja temos um processador que lê os operandos da memória de dados, de seguida, a sua unidade de dados inclui um fator de soma que a efetua e produz um resultada, sendo esse mesmo armazenado na memória de dados.
Primeira versão
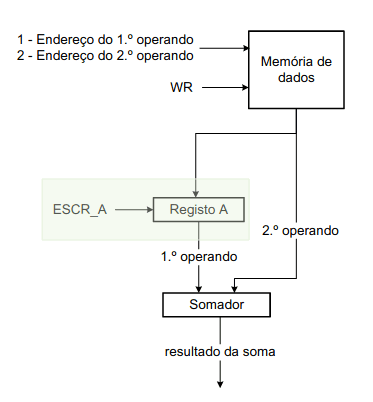
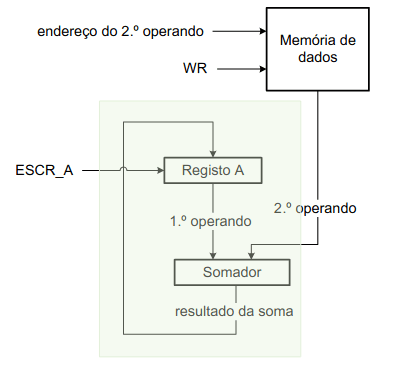
Já tendo conhecimento dos nossos objetivos, tratamos de um esquema para a nossa primeira versão.
Logo à partida percebemos que esta não pode ser a nossa versão final visto que o nosso somador tem duas entradas mas só uma saída. Para resolver esse problema temos que criar um registo que memoriza um dos operandos.
Assim, temos como controlo um sinal WR inativo e um sinal ESCR_A ativo para escrita no registo e desativo durante a operação de soma, visto estar só a ser lido.
Segunda versão
Vendo o nosso erro, criamos uma segunda versão.
Contudo, esta não poderá ser a nossa versão final visto que o nosso resultado não pode ir para a memória pois está ocupado a ler o segundo operando. A solução é simples: temos que usar o nosso registo para esse efeito, assim podemos compreender porque é que o registo tradicionalmente se chama "acumulador".
Logo, o nosso controlo será quando o sinal do relógio muda ESCR_A que fica ativo.
Terceira versão
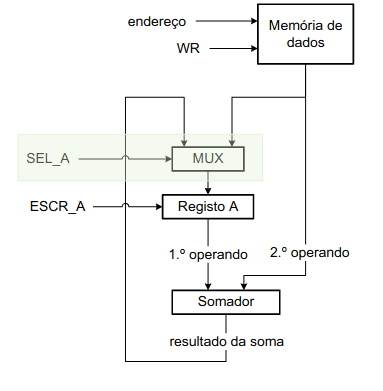
Chegamos, então, a uma terceira versão da nossa unidade de dados.
Vemos, contudo, que a nossa entrada do registo não pode vir de dois lados, isto é do registo e do somador, então temos que usar um multiplexer que nos permite selecionar a entrada.
O controlo nesta versão será o sinal SEL_A que define qual das entradas usar a cada momento.
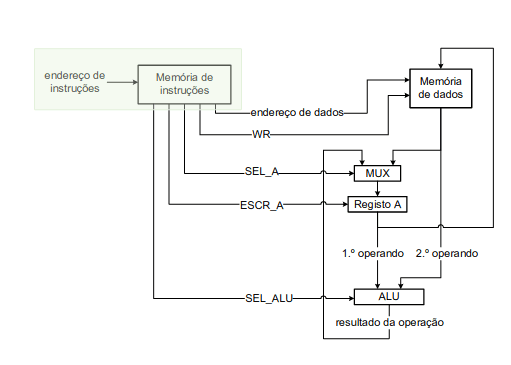
Quarta versão
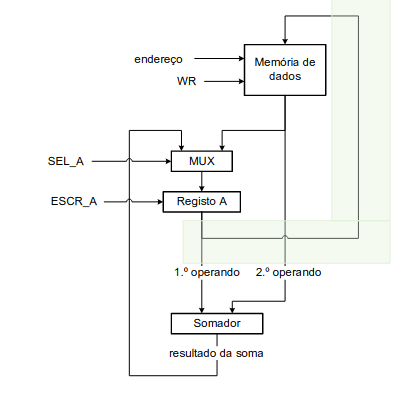
Na nossa quarta versão já estamos a contar com um multiplexer que nos auxilia a selecionar entradas.
Ao avaliarmos a nossa nova versão deparamos-nos com uma questão: como podemos guardar os nossos resultados na memória? A solução é ligar a saída do registo à entrada da memória, assim, o resultado vai sempre para o registo e depois copia-se.
Evidentemente, o nosso controlo é através da ativação do sinal WR.
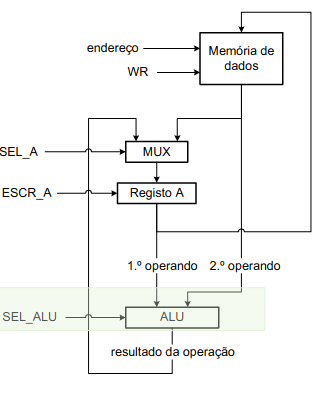
Quinta Versão
Já temos uma versão mais próxima da correta, contudo a nossa quinta versão ainda gera um problema: como suportamos várias operações? A resposta vem de um novo componente, a ALU (Arithmetic and Logic Unit). Este circuito digital tem como objetivo realizar as operações de adição e a operação booleana AND. Para podermos controlar este novo elemento precisamos de ter como controlo o sinal SEL_ALU que seleciona a operação.
Sexta versão
Já tendo uma ALU, temos agora que nos focar em como especificar o valor dos sinais que controlam o circuito. Isto pode ser completando se, a cada instrução, ou seja o conteúdo de uma célula na memória de instruções, deve especificar todos os sinais necessários para se executar.
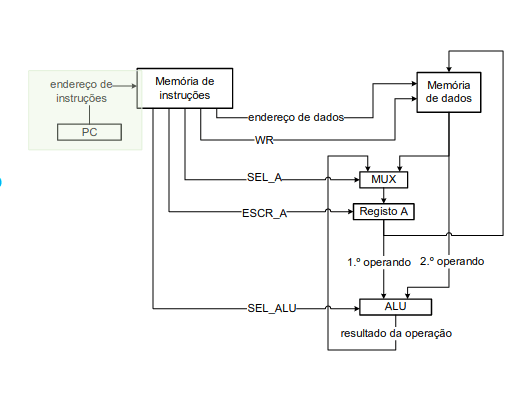
Sétima versão
Por fim só nos falta indicar quais as instruções e o seu sequenciamento que se pretende executar num dado programa. Para tal precisamos de utilizar um registo (program counter) que nos indica quais das instruções da memória de instruções da memória de instruções está em execução e um mecanismo que indique qual a instrução seguinte.
Primeiro programa!
Assim, finalmente já conseguimos fazer um programa que soma um número com todos os inteiros positivos menores que ele, ou seja
Este programa precisa de ter uma série de comandos:
- soma 0 (inicializamos a soma com zero)
- iteracao N (inicializa iteracao com N)
- Se (iteracao < 0) salta para 8
- Se (iteracao = 0) salta para 8
- soma soma + iteracao (adiciona iteracao a soma)
- iteracao iteracao -1 (decrementa iteracao)
- Sata para 4
- Salta para 8 (fim do programa)
Como podemos identificar, a soma e a iteracao são células de memória cujo conteúdo vai variando ao longo do tempo. Assim, cada célula de memória tem um endereço. Neste exemplo vamos pôr soma em 40H e iteracao em 41H.
- M[40H] 0 (inicializamos a soma com zero)
- M[41H] N (inicializa iteracao com N)
- Se (M[41H] < 0) salta para 8
- Se (M[41H] = 0) salta para 8
- M[40H] M[40H] + M[41H] (adiciona iteracao a soma)
- M[41H] M[41H] -1 (decrementa iteracao)
- Sata para 4
- Salta para 8 (fim do programa)
Porém, para facilitar o nosso programa podemos usar constantes simbólicas, isto é, identificar com um valor uma vez no início do nosso programa e podemos usar esta constante no nosso programa como se fosse o número com que foram definidas.
soma EQU 40H (definição do endereço da variável soma)
iteracao EQU 41H (definição do endereço da variável iteracao)
- M[soma] 0 (inicializamos a soma com zero)
- M[iteracao] N (inicializa iteracao com N)
- Se (M[iteracao] < 0) salta para 8
- Se (M[iteracao] = 0) salta para 8
- M[soma] M[soma] + M[iteracao] (adiciona iteracao a soma)
- M[iteracao] M[iteracao] -1 (decrementa iteracao)
- Sata para 4
- Salta para 8 (fim do programa)
Assim, podemos concluir que as variáveis ficam em memória de dados, as instruções ficam na memória de instruções, a cada passo do algoritmo temos uma instrução e o número do passo é o endereço na memória de instruções
Contador de Programa
Ainda avaliando o nosso programa de somas, podemos inserir um novo elemento: PC (contador de programa). O PC vai evoluindo instrução a instrução, tendo em conta que os endereços de memória começam em 0 e não em 1, e, após cada instrução, o PC contém o endereço da instrução seguinte. Por isso, quando fazemos um "salto", estamos somente a escrever um novo valor no PC.
soma EQU 40H (definição do endereço da variável soma)
iteracao EQU 41H (definição do endereço da variável iteracao)
- M[soma] 0 (inicializamos a soma com zero)
- M[iteracao] N (inicializa iteracao com N)
- Se (M[iteracao] < 0) PC 7
- Se (M[iteracao] = 0) PC 7
- M[soma] M[soma] + M[iteracao] (adiciona iteracao a soma)
- M[iteracao] M[iteracao] -1 (decrementa iteracao)
- PC 3
- PC 7 (fim do programa)
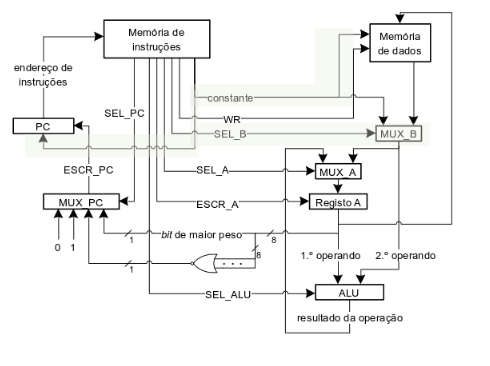
O meu primeiro computador
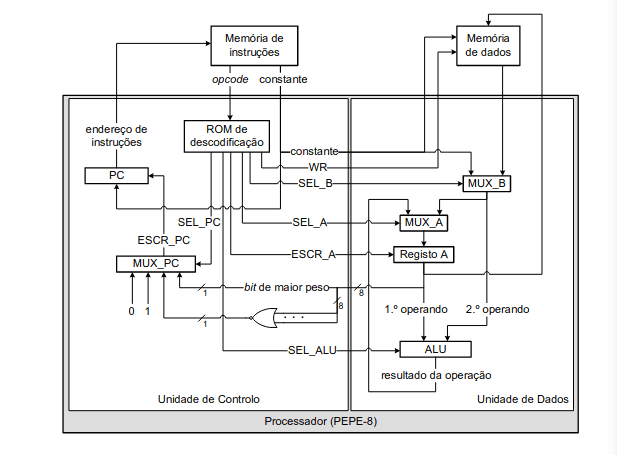
No esquema apresentado conseguimos identificar que a nossa constante também é usada para endereços; MUX_B suporta ops que guardam constantes no registo A e ops em que o 2º operando é uma constante; sinal SEL_B controla a seleção; a entrada do PC já permite saltos em que a constante especifica o novo endereço; para suportar saltos condicionais adiciona-se um multiplexer MUX_PC que é controlado por sinal SEL_PC.
O programa pode saltar em três situações diferentes:
- 01 representa um salto incondicional, ou seja salta sempre para endereço na constante, como é no caso de PC 7;
- 10 representa um salto apenas quando A=0, ou seja é um salto condicionado;
- 11 representa outro salto condicionado quando A<0, ou seja, quando é negativo
Programação em baixo nível
Aplicando diretamente à cadeira de IAC, em PEPE-8, a linguagem de Assembly que vamos utilizar durante as aulas, sabemos que há 256 combinações possíveis dos sinais de controlo, mas apenas 15 desta instruções são relevantes. Sabendo que não precisamos de indicar os 8 bits dos sinais, basta termos um opcode de 4 bits que nos permite selecionar a instrução.
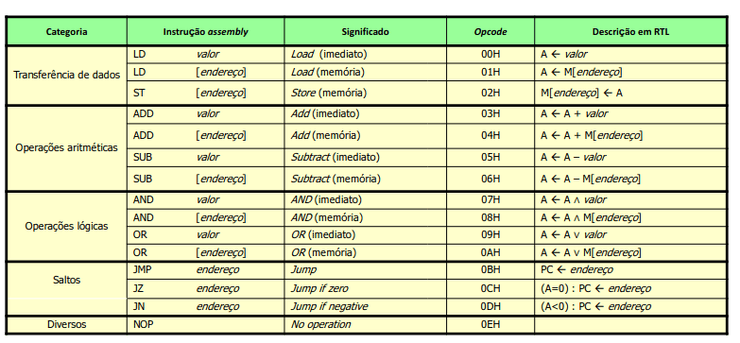
Programação em Assembly
Para programar precisamos de saber quais os comandos que podemos utilizar, assim, a tabela abaixo contém algumas instruções mais relevantes para a nossa aprendizagem da língua.
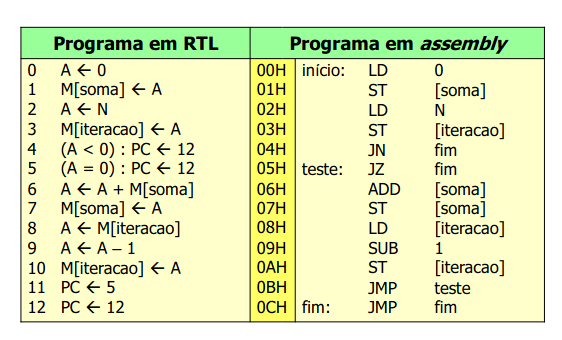
Logo, já podemos escrever um programa em PEPE que representa o nosso programa de somas descrito acima.
warning
Para outro exemplo de um programa em Assembly, é recomendada a leitura dos slides das teóricas.