Árvores Binárias
Árvores de Procura Binárias (BST)
As binary search trees, BSTs, têm por base uma lógica bastante simples: considerando o nó atual como sendo a raiz de uma árvore, todos os nós que partem do seu filho esquerdo (inclusive) têm chave menor que a sua, e todos os nós que partem do seu filho direito (inclusive) têm chave maior que a sua. Estamos, portanto, perante uma abordagem recursiva ao problema, já que cada nó é a raiz de uma sub-árvore da árvore "maior", e cada sub-árvore tem de respeitar também este princípio.
A pesquisa de um dado nó pela árvore é sempre iniciada a partir da raiz. Verifica-se necessariamente uma de três situações:
- A chave do nó atual é menor que a chave pesquisada. Nesse caso, a pesquisa continua a partir do filho direito do nó atual;
- A chave do nó atual é maior que a chave pesquisada. Nesse caso, a pesquisa continua a partir do filho esquerdo do nó atual;
- A chave do nó atual é igual a chave pesquisada. Nesse caso, o nó atual é o nó desejado, e podemos parar a procura.
Caso cheguemos ao nó nulo, NULL em C, nenhum nó na árvore tem a chave pretendida, pelo que a pesquisa não teve sucesso.
Inserir um nó na árvore tem uma lógica-base semelhante, com alguns twists pelo meio. Iniciamos uma espécie de "procura" na raiz, e o objetivo será percorrer a árvore de cima para baixo, até encontrarmos o lugar certo para introduzir o novo elemento. Este lugar certo será o local onde tivermos encontrado NULL. Tal deve-se a à própria procura, tal como explicada acima, acabar por indiretamente descobrir o sítio correto de inserção da chave a procurar caso esta não seja encontrada: procurámos o caminho certo para encontrar a chave, caso ela estivesse na árvore, e não a encontrámos; se não está lá, então este será o local correto para a inserirmos!
Remover um elemento é bastante simples. Realizamos uma procura normal, e assim que encontrarmos o nó pretendido (seja esse nó ):
- Caso não tenha filhos, basta apenas apagá-lo;
- Caso tenha apenas um filho, redirecionamos o pai de para o seu filho e apagamos .
- Caso tenha dois filhos, substituímo-lo pelo maior dos elementos à sua esquerda e apagamo-lo da sua posição original.
Elementos Máximo e Minímo
Para encontrar o elemento com chave mais elevada, devemos procurar o elemento mais à direita da árvore; pelo contrário, para encontrar o elemento com chave mais baixa, devemos procurar o elemento mais à esquerda.
link max(link h) {
if (h == NULL || h->r == NULL) {
return h;
} else {
return max(h->r);
}
}
link min(link h) {
if (h == NULL || h->l == NULL) {
return h;
} else {
return min(h->l);
}
}Travessias pela Árvore
Travessia Pre-Order
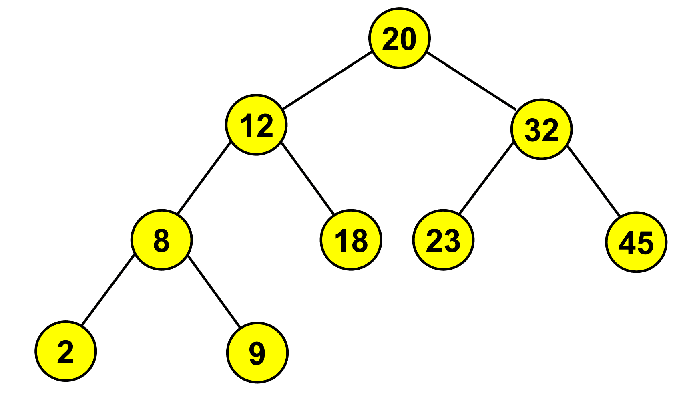
Numa travessia pre-order, visitamos sempre a raiz antes de visitar os seus filhos (com visita entenda-se "guardar/imprimir o valor do nó"). Pegando na árvore acima, uma travessia pre-order pela mesma produziria um output 20, 12, 8, 2, 9, 18, 32, 23, 45.
Travessia In-Order
Numa travessia in-order, visitamos sempre a raiz depois de visitar o filho à esquerda e antes de visitar o filho à direita. Pegando na árvore acima, uma travessia in-order pela mesma produziria um output 2, 8, 9, 12, 18, 20, 23, 32, 45. Em BSTs, esta travessia produzirá um output ordenado de forma crescente!
Travessia Post-Order
Numa travessia post-order, visitamos sempre a raiz depois de visitar os seus filhos. Pegando na árvore acima, uma travessia post-order pela mesma produziria um output 2, 9, 8, 18, 12, 23, 45, 32, 20.
Árvores Binárias Equilibradas
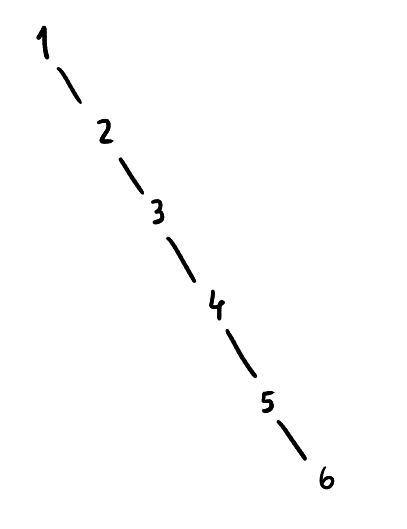
As pesquisas em árvores de procura binária são, por norma, realizadas de forma eficiente (. O pior caso, contudo, é linear: basta olhar para o caso em que inserimos, por esta ordem, 1, 2, 3, 4, 5, 6. Nesse caso, ficamos com uma árvore deste tipo:
Esta árvore é, claro, desiquilibrada, podendo assim ficar até atrás de vetores ordenados (quando acompanhados de pesquisa binária). Assim sendo, fará sentido encontrar maneiras de equilibrar a árvore.
Árvores equilibradas têm como principal objetivo reduzir a complexidade temporal no pior caso de pesquisa na mesma, a troco de complexidade adicional na construção e manutenção das mesmas (através da técnica de reequilibragem).
As BSTs equilibradas mais comuns são as Red-Black e as AVL, sendo que em IAED abordamos por norma estas últimas.
Árvores AVL (Adelson-Velsky and Landis)
Nas árvores AVL, todas as operações têm complexidade temporal associada , dado serem árvores equilibradas. Este equilíbrio é atingido através de um princípio relativamente simples: para todo o nó da árvore, a altura/profundidade de cada filho difere em no máximo 1 unidade. A noção de profundidade está aqui associada à distância (quantidade de nós) até à folha da árvore mais profunda (passo a redundância). Normalmente, referimo-nos a esta diferença entre as alturas dos filhos como Balance Factor, ou Fator de Equilíbrio, dado trivialmente por height(left) - height(right).
A cada inserção e remoção de um nó da árvore AVL, há a possibilidade da árvore ficar desiquilibrada: para o combater, cada vez que uma dessas operações é executada temos de verificar possíveis desiquilíbrios que tenham sido criados, e aplicar rotações (algo que vamos explorar mais à frente) para os resolver. Esta necessidade frequente de rotações e equilíbrios adiciona uma camada adicional de complexidade à implementação da árvore, pelo que em casos onde tempos logarítmicos não são um must, é frequente utilizar uma implementação naíve de árvores binárias.
Inserir um nó na árvore AVL
Inserir um elemento numa árvore AVL é uma operação separada em duas fases: uma primeira, a de procura do lugar onde inserir o elemento, realizada tal como se de uma árvore binária "normal" se tratasse; uma segunda, onde temos de verificar se a inserção do elemento na árvore causou desiquilíbrios (e caso tal tenha acontecido, corrigi-los).
O processo de correção é iniciado a partir da folha que acabou de ser inserida na árvore. Vamos procurar subir na árvore, até encontrar um nó onde o fator de equilíbrio seja maior que (em módulo). Quando tal ocorrer, vamos realizar uma rotação, simples ou dupla, no nó em "incumprimento" para corrigir o desiquilíbrio. Assim que equilibrarmos o nó, podemos parar de subir - todo o resto da árvore para cima estará também em cumprimento.
Apesar de parecer óbvio mesmo sem o mencionar, podemos notar que caso consigamos subir da folha até à raiz sem necessidade de rotações, podemos dizer que a inserção do novo elemento não desiquilibrou a árvore.
Já falámos várias vezes de rotações, mas ainda não nos demos ao trabalho de as definir: continua a ser uma incógnita como funcionam e como de facto conseguem equilibrar as nossas árvores binárias. Vamos, portanto, apresentar dois pares de rotações, simples e duplas:
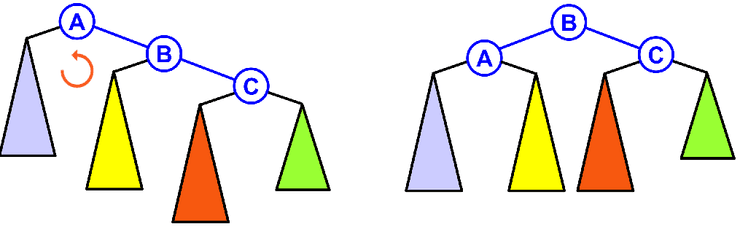
Rotação Simples - Left
Precisamos de fazer uma rotação à esquerda quando inserimos um nó na sub-árvore direita de uma sub-árvore direita.
link rotL(link h) {
link x = h->r;
h->r = x->l;
x->l = h;
return x;
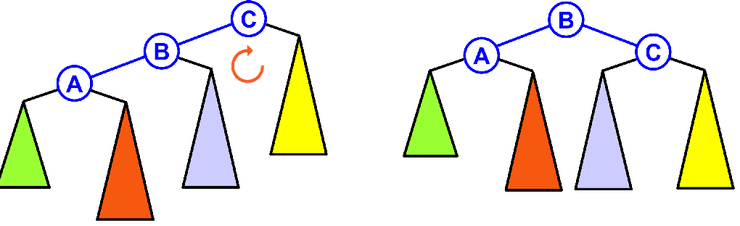
}Rotação Simples - Right
Precisamos de fazer uma rotação à direita quando inserimos um nó na sub-árvore esquerda de uma sub-árvore esquerda.
link rotR(link h) {
link x = h->l;
h->l = x->r;
x->r = h;
return x;
}As rotações duplas são utilizadas quando uma só rotação não chega para voltar a colocar a árvore em equilíbrio.
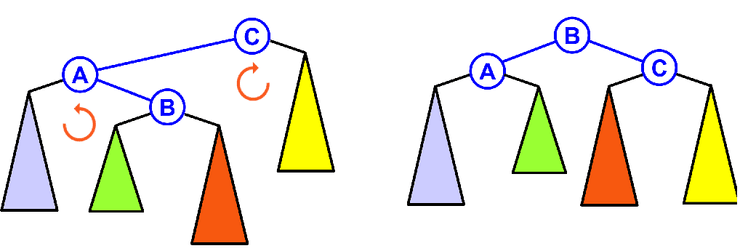
Rotação Dupla - Left-Right
Consiste em fazer duas rotações simples de seguida, primeiro uma à esquerda e outra à direita (realizamos uma primeira rotação, mas o balance factor continua maior que ). Fazemos esta operação caso tenhamos inserido um nó na sub-árvore direita de uma sub-árvore esquerda.
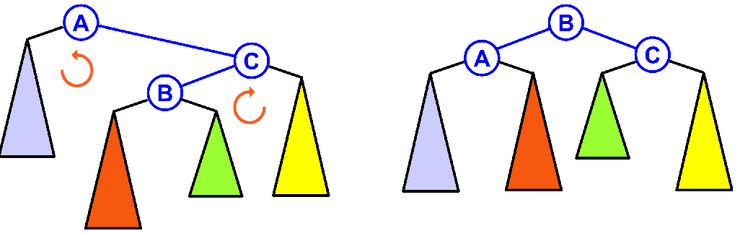
Rotação Dupla - Right-Left
Consiste em fazer duas rotações simples de seguida, primeiro uma à direita e outra à esquerda. Fazemos esta operação caso tenhamos inserido um nó na sub-árvore esquerda de uma sub-árvore direita.
Remover um nó da árvore AVL
A remoção inicia-se tal como numa BST normal: fazemos a pesquisa inicial para encontrar o nó pretendido e removê-lo. O que difere é o que vem a seguir - aqui, não basta apenas ligar o pai do nó removido a um dos seus filhos (já que tal pode, sem mais verificações, resultar em árvores desiquilibradas). O processo será, aqui, semelhante ao da inserção de um nó na AVL: subimos até à raiz com vista a encontrar nós em desiquilíbrio, equilibrando-os sempre que necessário. Contudo, ao contrário da inserção, vamos sempre subir até à raiz, independentemente de já termos equilibrado nós mais abaixo ou não - aqui, poderá ser necessário equilibrar sub-árvores ascendentes.
Desempenho em AVLs
Tal como referido no início desta sub-secção, todas as operações principais são feitas em tempo logarítmico. Tal é verdade, já que temos:
- Equilibragem (rotações simples e duplas) - .
- Pesquisa - .
- Inserção - . Temos que a procura inicial é realizada em tempo logarítmico e que subir pela árvore leva também operações no pior caso (e a equilibragem é feita em tempo constante).
- Remoção - . Temos que a procura inicial é realizada em tempo logarítmico e que subir pela árvore leva também operações no pior caso. Sendo que, no pior caso, todos os nós terão de ser equilibrados, subir e equilibrar os nós levará tempo (que, claro, continua a ser logarítmico).