Tabelas de Dispersão (Hash Tables)
Tabelas de Dispersão
Ao longo do tempo, vamos encontrar situações em que precisamos que operações de procura, inserção e remoção de elementos seja feita, em média, em tempo constante. Se os elementos não tiverem necessariamente de ter uma relação de ordem entre eles, podemos usar tabelas de dispersão, em inglês hash tables, para esse efeito. Já contactámos com hash tables, mesmo sem saber, na cadeira de FP - dicionários em Python são implementações de hash tables.
Função de Dispersão (Hashing)
Como funciona então a dispersão - como é que conseguimos tempos, em média, tão bons?
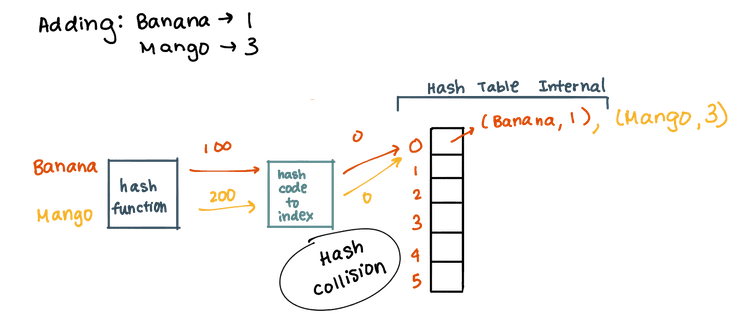
Bem, estes tempos são atingidos através de hashing: uma técnica que recorre a uma função de dispersão, função essa que recebe um dado elemento e retorna um índice na hash table. Esta função deve, idealmente, ser:
- rápida de calcular: caso contrário, o tempo ganho ao usar tabelas de dispersão seria contrariado pelo hashing.
- envolver todos os bits da chave: idealmente, nenhum pedaço do input deve ser inutilizado, de forma a obter um hashing que seja único para cada elemento.
- deve distribuir as chaves de forma uniforme e quase aleatória: numa função de dispersão ideal, a probabilidade de ocorrer uma colisão (a função devolver o mesmo índice para dois elementos distintos) deve ser , onde é o tamanho da tabela.
Utilizamos, claro, funções de dispersão diferentes para elementos de tipos diferentes: um hashing para cadeias de caracteres não será o mesmo do que o utilizado para números reais, por exemplo.
Quando estamos a trabalhar com números, é usual a nossa hash function trabalhar com o módulo (resto) do elemento, k % M - desta maneira, considerando no máximo elementos, não deverá haver colisões. Devemos idealmente fazer uma estimativa conservadora para o tamanho da tabela, de forma a não ser apanhados de surpresa com quantidades anormais de colisões.
int hash_int(int value, int M) {
return value % M;
}Trabalhar com cadeias de caracteres requer uma estratégia diferente - não existe o "módulo de uma string", pelo que temos de adaptar a nossa hash function. O nosso objetivo, aqui, passa por calcular uma soma ponderada dos caracteres: uma maneira de o fazer é, por exemplo:
int hash_string(char *v, int M) {
int h = 0, a = 127;
for (; *v != '\0'; v++) {
h = (a * h + *v) % M;
}
return h;
}Notem-se que esta é uma implementação possível para uma hash function que trabalha com cadeias de caracteres, estando longe de ser a única. Pela internet fora existem inúmeras outras implementações, pelo que sugiro que procurem outras caso esta não se adeque ao vosso problema. Mais ainda, resta referir que devemos sempre recorrer a "valores auxiliares" primos, já que estes reduzem bastante o risco de colisão.
Também podemos recalcular a base a cada iteração do loop principal, de modo a evitar anomalias com chaves altamente regulares:
int hash_string_2(char *v, int M) {
long int h, a = 31415, b = 27183;
for (h = 0; *v != '\0'; v++, a = a * b % (M-1)) {
h = (a * h + *v) % M;
}
return h;
}Como Resolver Colisões?
Já vimos que podem ocorrer colisões, caso a hash function retorne o mesmo índice para elementos diferentes. Não vimos, contudo, como resolvê-las - não podemos, claro, "substituir" o elemento que lá estava pelo novo, temos de arranjar maneira de ter ambos na tabela. Existem algumas maneiras diferentes de resolver este problema.
* Os slides que acompanham a cadeira costumam conter o código utilizado para implementar estas estratégias de resolução de colisões (e implementações de hash tables em geral). Dado serem trechos bastante extensos de código, não serão incluídos nesta página.
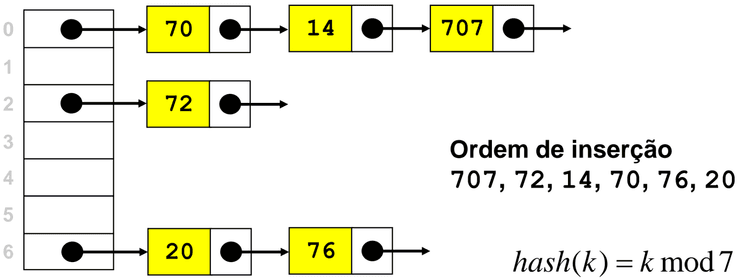
Resolução via Encadeamento Externo (Separate Chaining)
Aqui, cada posição da tabela tem um ponteiro para uma lista: desta forma, as colisões são resolvidas juntando o novo elemento ao início da lista. As remoções são realizadas removendo o elemento da lista. Aqui, o comprimento médio das listas será , para e . Apesar de o pior caso ser linear - acontece caso todos os elementos tenham o mesmo índice associado - este pior caso tem probabilidade baixíssima de ocorrer, pelo que em média mantêm-se tempos de acesso "baratos".
Resolução via Procura Linear (Linear Probing)
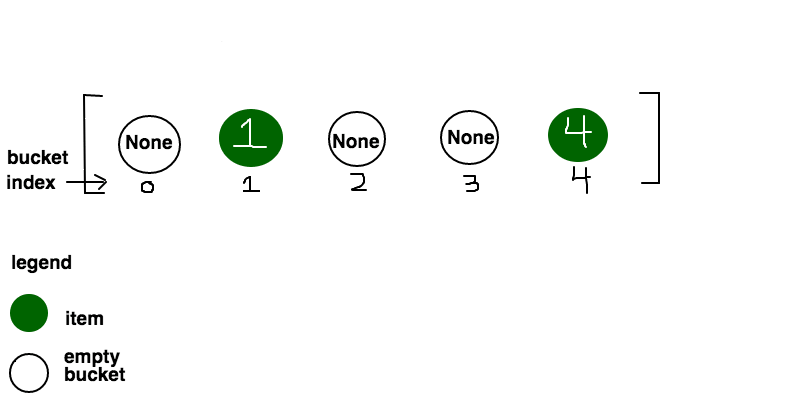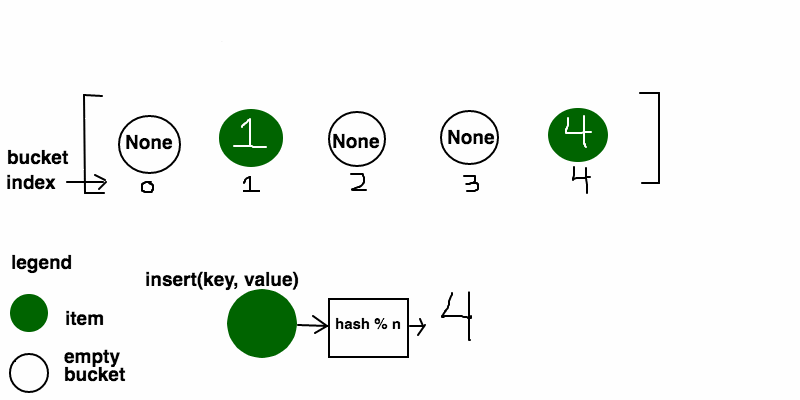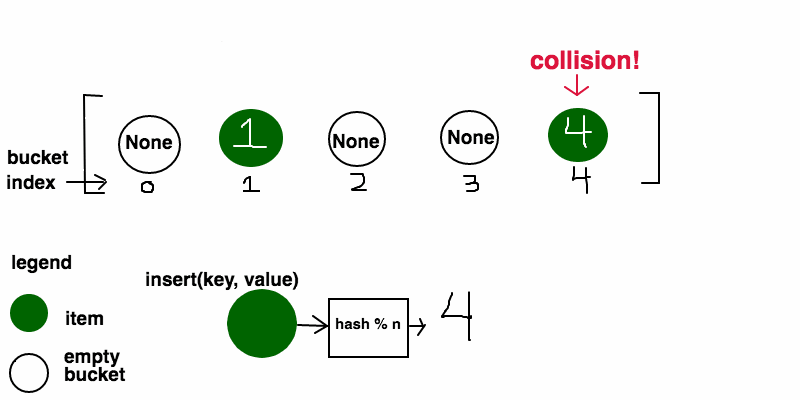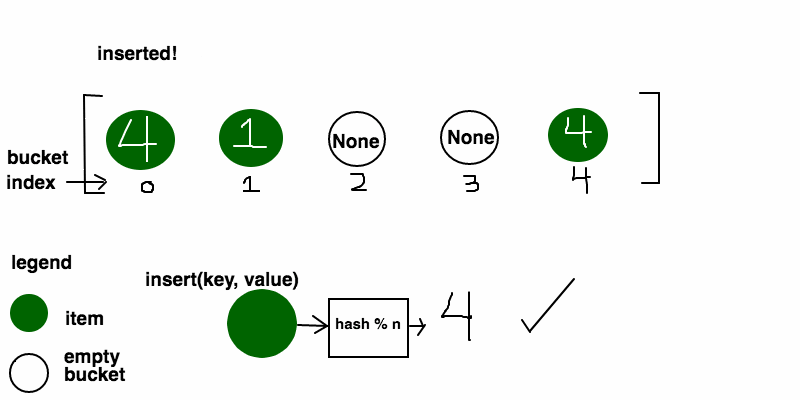
Aqui, cada posição da tabela guarda no máximo um elemento. Se calcularmos um índice mas a tabela já lá contiver um elemento, devemos continuar a mover-nos pela tabela até ao fim, até encontrar um espaço livre (inserindo-o nesse espaço). A procura e remoção de elementos funcionam todas desta maneira: calcula-se o índice e verifica-se se o elemento está lá; caso não esteja, continuamos a avançar pela tabela até encontrar uma posição vazia (caso encontremos uma posição vazia antes de encontrar o elemento pretendido, o elemento não está na tabela). No caso da remoção de um elemento, após remover o elemento, devemos reorganizar a tabela atualizando os índices dos seus elementos:
- Após achar o elemento a remover (caso exista) colocar essa posição a NULL (ou qualquer valor que sinalize a posição como livre) e reinserir todos os elementos adjacentes até encontrar uma posição vazia.
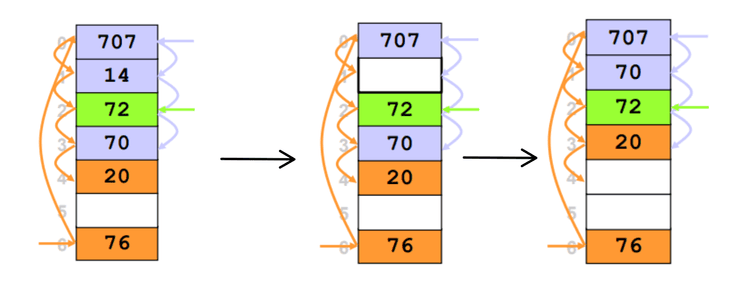
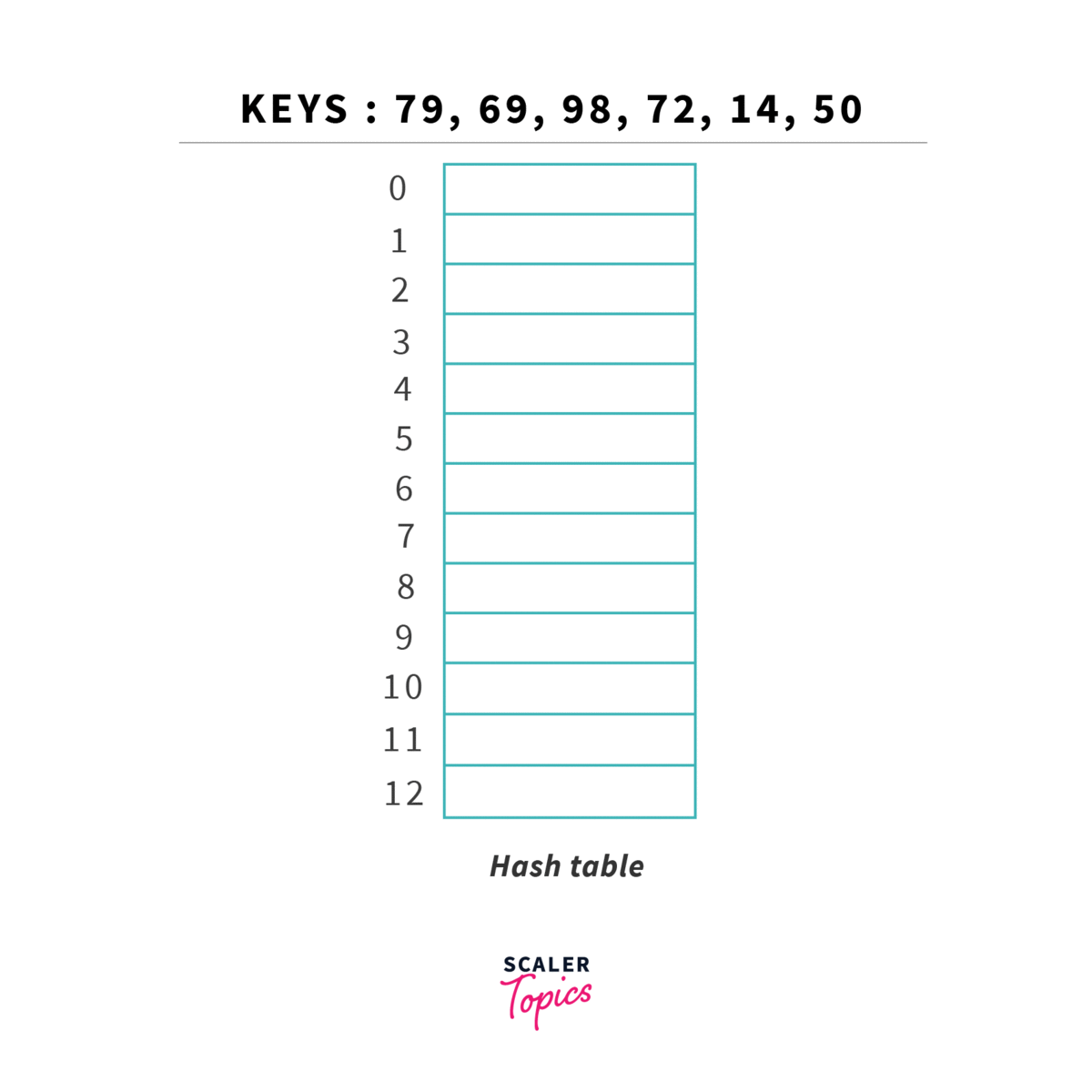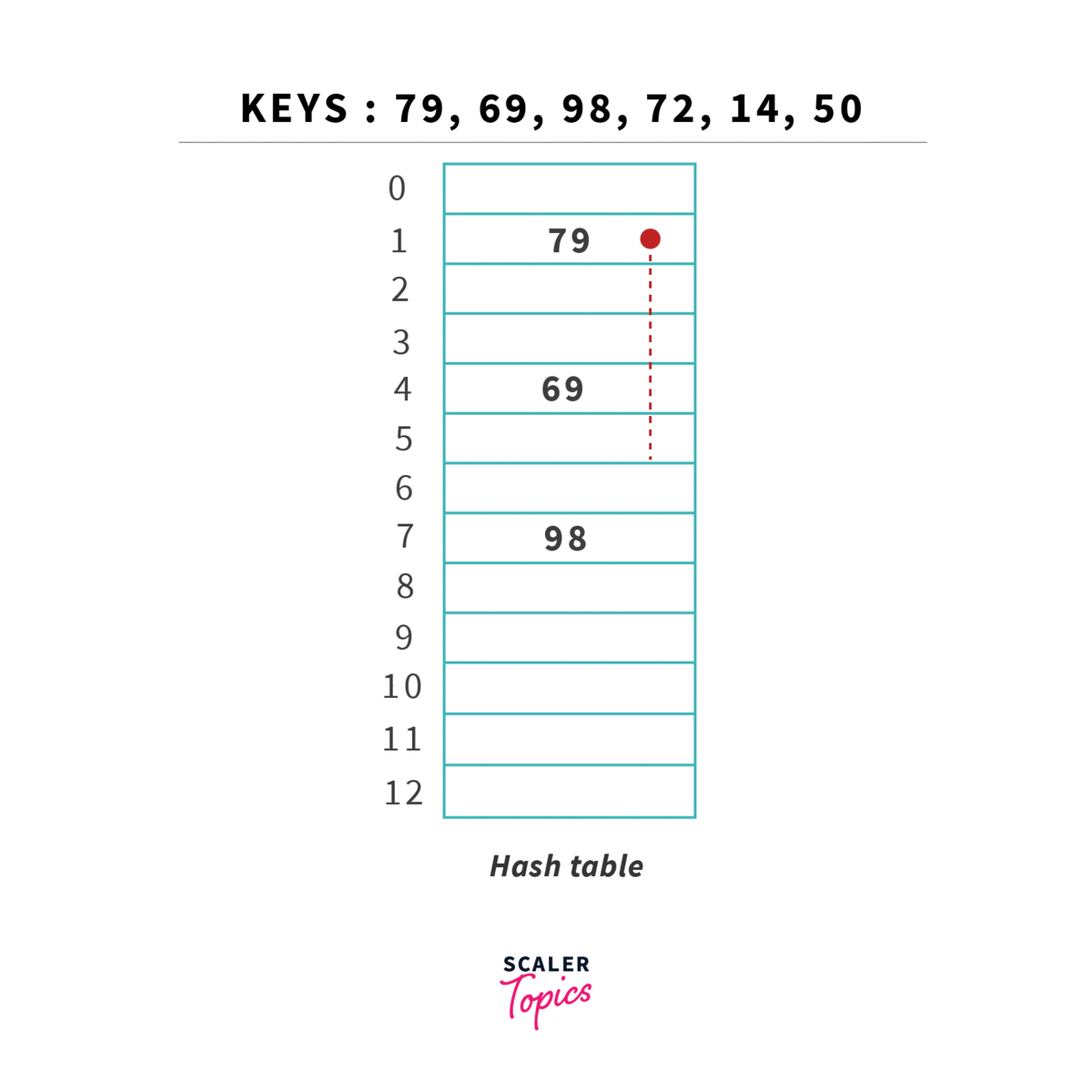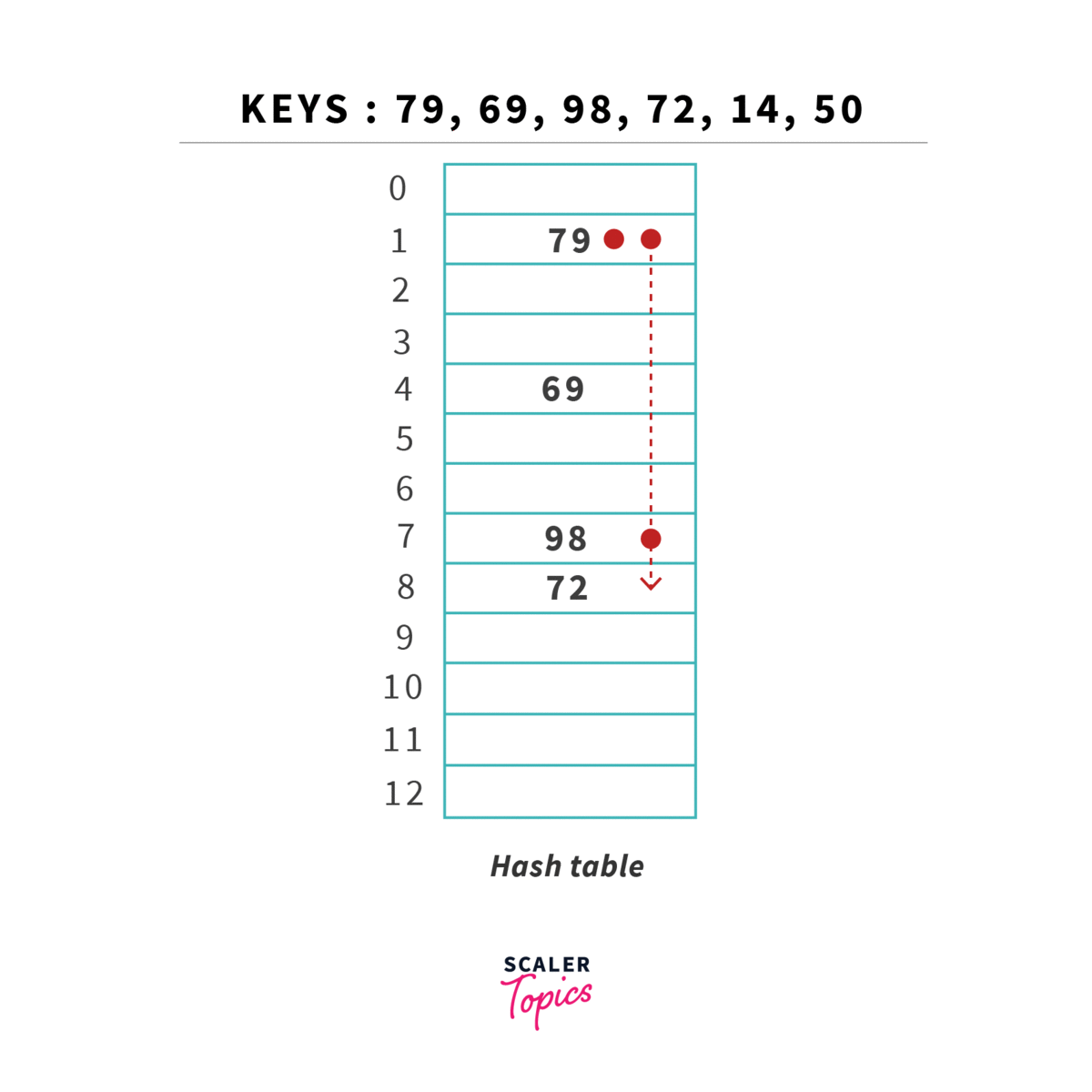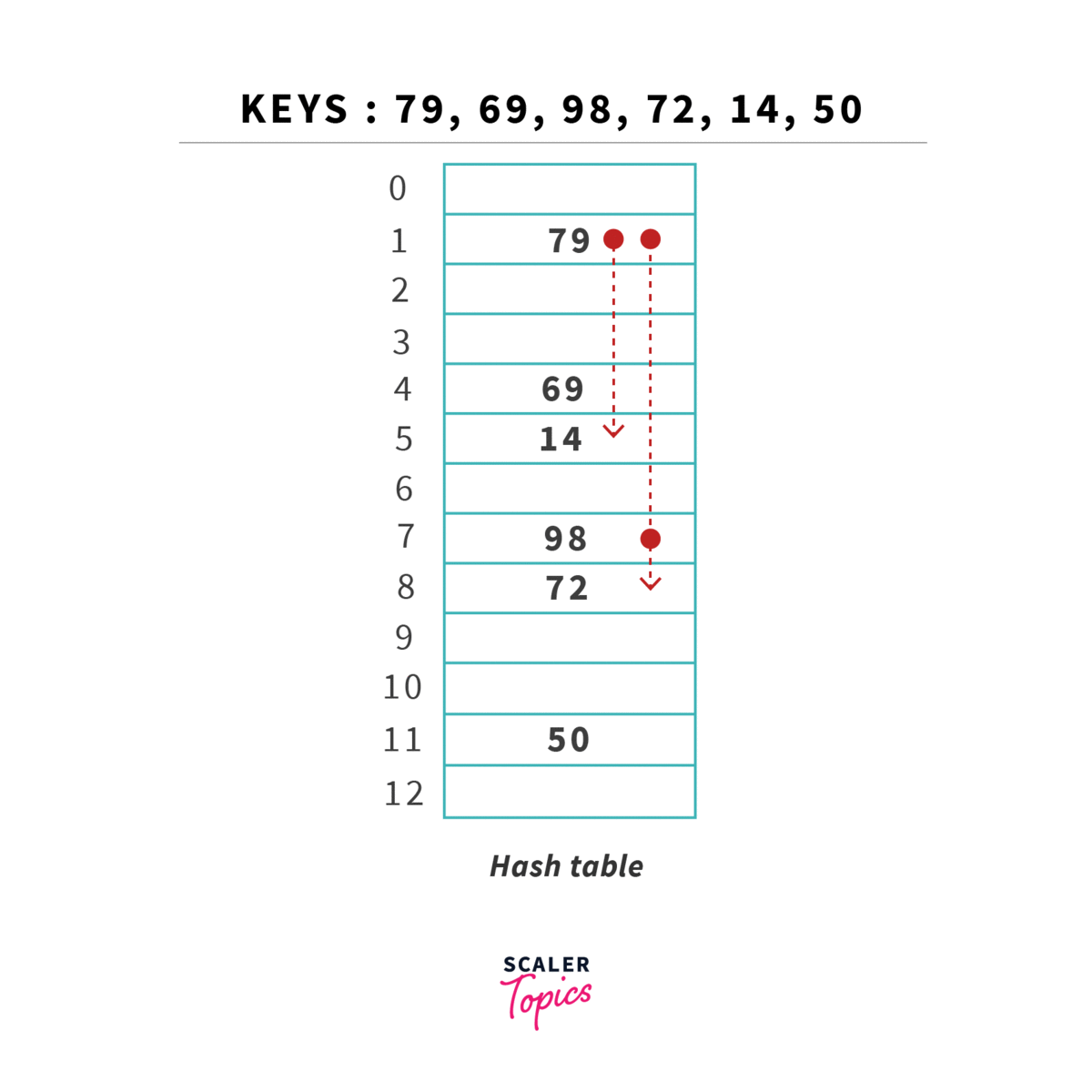
O exemplo seguinte pode ajudar a entender o que acontece. Removemos da posição . Em seguida vamos reinserir todos os elementos adjacentes até à primeira posição vazia. Neste caso fica na mesma posição (pois já se encontra na posição do seu índice), contudo, após reinserirmos a sua posição muda, bem como a posição de , isto acontece pois existiu libertação de posições na tabela com índices iguais ou posteriores aos dos índices destes elementos. A reorganização da tabela é terminada quando se encontra a primeira posição vazia, neste caso, a posição no índice .
A estratégia em questão requer que se saiba o número de elementos a inserir à priori! Caso contrário, podíamos ficar sem espaço para inserir elementos na tabela. Mais ainda, tem de ser idealmente menor que , já que o número de operações necessárias para encontrar um elemento na tabela é dado por:
-
Hits:
-
Misses:
O número de operações cresce rapidamente quando .
Resolução via Double Hashing
Tal como na procura linear, vamos sempre procurar guardar elementos na tabela em si, sem recorrer a estruturas auxiliares (como listas ou similares). Vamos, contudo, utilizar outra técnica para resolver conflitos: em vez de procurar sequencialmente a próxima posição vazia, vamos utilizar uma segunda hash function para determinar o incremento ao índice originalmente obtido. Este incremento deverá ser sempre primo relativamente ao tamanho da tabela.
Esta estratégia permite diminuir o número de operações relativamente à procura linear, tendo apenas problemas quanto à sua eficiência caso a tabela esteja muito cheia (load superior a ), já que vamos ter de calcular hashes repetidos várias vezes. Tal como em linear probing, deve ser menor que 1. O número de operações necessárias para encontrar um elemento é dado por:
-
Hits:
-
Misses:
Como podemos ver, mesmo para perto de , o número de hits e misses cresce de forma muito mais controlada que na procura linear!
Tabelas de Dispersão Dinâmicas
Em hash tables regular, o aumentar da carga (isto é, o número de elementos) na tabela leva também a um aumento do custo de inserção e procura de elementos. Em tabelas com encadeamento externo, este aumento é gradual - começamos com operações em tempo constante, podendo atingir piores casos lineares. No caso da procura linear e double hashing, os custos vão também aumentando, à medida que vamos tendo de procurar por mais sítios diferentes para colocar os elementos.
Para evitar tempos incomportáveis de inserção, remoção e procura de elementos, é costume utilizar-se tabelas de dispersão dinâmicas: assim que a tabela estiver meio cheia, duplicamos o seu tamanho. Esta duplicação não é uma operação barata - temos de fazer re-hash dos nossos elementos para os colocar na nova tabela. É, contudo, uma operação pouco frequente (isto considerando que inicializámos a tabela com um tamanho conservador), pelo que os ganhos acabam por superar essa perda.
As tabelas de dispersão concretizam, então, operações de inserção e procura em tempo constante (em média). Não têm, contudo, garantia de desempenho: há sempre a possibilidade (ainda que pouco comum) de uma operação levar tempo linear a ser concretizada. O custo do hashing pode ainda ser relativamente caro para o caso de chaves muito longas, e há obviamente o elefante na sala: estas tabelas ocupam por natureza muito mais memória do que o necessário, um trade-off necessário para encurtar os tempos médios que as operações levam. Devemos, portanto, ter sempre em consideração se as especificações do problema que nos é proposto têm limitações apertadas de memória: se assim for, talvez seja boa ideia partir para outras estruturas, mesmo acabando por perder desempenho.
Em suma:
- A procura linear é a estratégia mais rápida, quando temos tabelas esparsas;
- O double hashing acaba por ser o melhor compromisso tempo/memória, já que não só não utilizamos estruturas de dados auxiliares como não procuramos elementos sequencialmente;
- O encadeamento externo é o mais fácil de implementar, sofrendo contudo aumentos graduais de desempenho e acabando por ocupar bastante memória.
Podem ainda ler este artigo sobre tabelas de dispersão dinâmicas, que explora estas e outras estratégias de resolução de colisões em tabelas de dispersão.