Conexionistas
Responsáveis pela origem do deep learning, os conexionistas defendem uma aprendizagem conseguida pela simulação do funcionamento do cérebro humano. Assim, existe uma representação computacional do cérebro, mais concretamente dos neurónios e das ligações entre eles. A aprendizagem dá-se no processo de mudança gradual na força das ligações entre os neurónios.
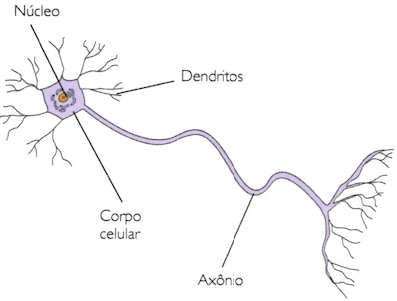
Um neurónio recebe o estímulo através das suas dendrites, processando os sinais e transmitindo os resultados a outros neurónios através do amónio. Contudo, o sinal só é transmitido se os estímulos recebidos ultrapassarem um determinado valor mínimo.
Perceptron
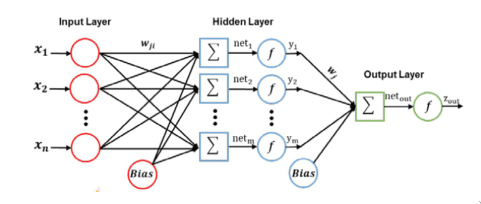
Cada neurónio é representado como uma função de variáveis, com o nome de entradas. O resultado é designado por saída. De modo a emular o funcionamento do neurónio, que dispara ou não dispara, é calculada uma função de ativação aplicada à net, que corresponde a uma soma ponderada das entradas. O objetivo do percetrão é, então, classificar uma entrada como pertencente a uma de duas classes: ou .
Processo de Treino
O processo de treino corresponde, então, ao ajuste gradual dos pesos , de modo à saída corresponder à classe do registo representado pelas entradas, minimizando uma função de erro. Na verdade, os parâmetros dos pesos correspondem a um hiperplano em dimensões. Este hiperplano separa as duas classes dos dados, que são representadas como pontos em dimensões, correspondentes aos registos dos dados.
A atualização dos pesos é feita de acordo com a regra seguinte, em que corresponde à learning rate, que determina o tamanho da variação efetuada aos pesos.
Note-se que representa o erro, que pode tomar valores 2, -2 ou 0.
Algoritmo
O algoritmo de treino do percetrão, abaixo descrito, converge para uma classificação correta se o conjunto de treino for linearmente separável e for suficientemente pequeno. É de notar que um valor demasiado pequeno de faz com que o algoritmo não tenha tanto em conta a contribuição de observações seguintes. Por outro lado, uma valor de demasiado grande pode desvalorizar as observações anteriormente consideradas. É necessário equilibrar estes dois conflitos.
- Inicializar os pesos com valores arbitrários.
- Escolher um registo .
- Calcular o valor de net.
- Calcular o valor do output = (net), em que é a função de ativação.
- Calcular e atualizar os pesos.
- Repetir a partir de 2. até não ser realizada nenhuma atualização aos pesos.
Limitações
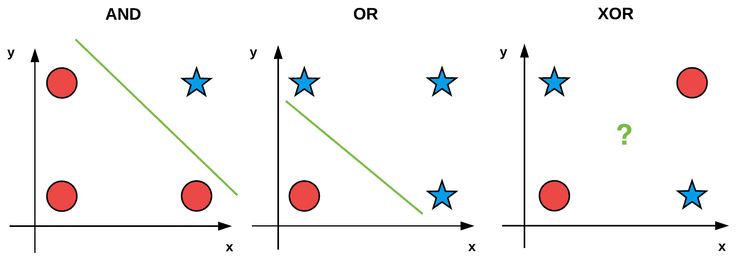
É de notar que este modelo apenas consegue representar conjuntos que sejam separáveis por uma linha, denominados conjuntos linearmente separáveis. Por exemplo, este é incapaz de aprender a operação de ou exclusivo (XOR), pois não há uma linha no plano que separe as classes correspondentes aos valores lógicos V e F.
Funções de Ativação
Existem várias funções de ativação. As mais relevantes encontram-se listadas a seguir.
- Sign Function
- Sigmoid Function
- Hyperbolic Tangent
- Softmax
Cross-Entropy
A função sigmóide, para o valor de , converte a sua entrada numa probabilidade, sendo o seu contradomínio . Assim, podemos converter o valor de net numa probabilidade. Pois na tarefa de classificação apenas existem duas classes, podemos realizar a seguinte interpretação:
Assim, os neurónios disparam com uma probabilidade e não disparam com uma probabilidade . Logo, o neurónio segue uma distribuição de Bernoulli.
Assumindo independência no conjunto de dados, podemos estimar os pesos do modelo tal que o likelihood seja maximizada. Assim, chegamos à expressão da função de erro da cross-entropy.
Gradient Descent
Este é um método numérico utilizado para determinar o mínimo da funções que não podem ser determinados algebricamente. O algoritmo começa por receber uma função a minimizar, e escolhe um vetor de pesos inicial, e, a cada iteração, soma este vetor a outro com sentido .
Assim, cada coordenada do vetor vê-se incrementada de acordo com a seguinte regra.
O processo continua até que o algoritmo convirja para um solução ( tem de ser pequeno o suficiente), pois o erro definido por contém apenas um mínimo global. Para um valor de muito grande, poderíamos sobrestimar o passo e passar para lá deste mínimo global.
Vertentes de Gradient Descent
Enquanto que o método de gradient descent atualiza os pesos depois de considerar todas as observações do conjunto de treino, calculando o erro acumulado, o método do stochastic gradient descent atualiza os pesos a cada observação do conjunto de treino.
Multi-Layer Perceptron
Motivação
De modo a conseguir que o percetrão consiga modelar a função XOR, podemos adicionar ao percetrão várias camadas, ditas intermédias ou escondidas (pois não conseguimos ver qual a sua saída), de modo a emular comportamentos mais complexos. A composição de percetrões são organizadas em camadas, em que as saídas de uma camada influenciam as entradas da camada seguinte. Daí este modelo ser conhecido como feed forwards network.
Contudo, múltiplas camadas de unidades lineares não deixam de poder apenas representar funções lineares. Para representar funções não lineares, necessitamos de funções de ativação não lineares. Assim, um percetrão multi camada com camadas escondidas consegue aproximar qualquer região contínua com um erro arbitrariamente pequeno. A camada de saída deste modelo pode ser treinada como se tratasse de um percetrão de uma só camada.
O percetrão simples apenas conseguia realizar classificação binária. Com várias camadas é agora possível realizar tarefas de classificação (com mais de duas classes) e regressão.
O objetivo passa por estimar um matrizes de pesos, , de modo a minimizar uma função de erro .
Notação
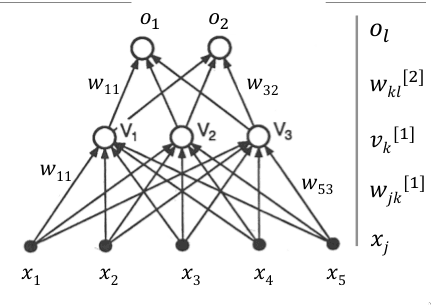
A primeira e última camada são a camada de entrada e a camada de saída, respetivamente. A camada de entrada recebe o índice 1. As entradas da primeira camada correspondem aos valores a , sendo o número de entradas. Existe também um termo de bias correspondente a . Na camada de saída, temos os valores das saídas, até .
Entre cada duas camadas adjacentes, existem ligações entre todos as unidades. Os valores destas ligações correspondem aos pesos. Define-se como a ligação entre as unidades , da camada e , cada camada . Os pesos da que ligam as unidades da camada à camada são representados por uma matriz, , com dimensões onde corresponde ao número de unidades da camada e corresponde ao número de unidades da camada .
De maneira semelhante, define-se como o k-ésimo elemento do vetor de output, , da camada .
Os valores de bias são representados separadamente, por razões práticas, em vetores , onde corresponde ao número da camada.
Forward Propagation
Este corresponde ao processo de, dada uma entrada, calcular a saída da última camada. Dada uma observação , a primeira camada escondida recebe uma entrada dada por
e calcula uma saída dada por
onde representa a função de ativação escolhida.
De uma forma geral, este processo pode ser escrito na seguinte fórmula geral, em que consideramos os valores de entrada, a observação como a saída da camada 0, .
O output da camada de saída, , num percetrão de camadas, corresponde à classificação final.
Backward Propagation
Este processo corresponde a, calculada a saída correspondente a uma entrada, calcular o erro da classificação e ajustar as várias matrizes de pesos adequadamente. Para tal, é aplicada um algoritmo de gradient descent, pois é diferenciável se a função de ativação também o for.
Transformações do Conjunto de Dados
As camadas escondidas deste modelo conseguem realizar transformações lineares ao conjunto de dados. Assim, além de aprender quais os melhores valores para o vetor de pesos, o modelo também aprende qual a melhor transformação a realizar ao conjunto de dados, de modo a minimizar a função de erro. Isto faz com que o MLP seja um modelo com bastante poder expressivo.
Overfitting
De modo a evitar o overfitting do MLP ao conjunto de dados, pode ser implementada uma política de early stoppng, onde o processo de treino é terminado antes que o modelo sofra de overfitting. As observações de treino são então divididas num conjunto de treino e noutro conjunto de validação. O processo de treino é interrompido quando o erro de teste aumenta durante iterações consecutivas.
Outra solução para este problema passa por adicionar um termo de regularização à função de erro.