Avaliação de Modelos de Regressão
À semelhança dos classificadores, os modelos de regressão podem ter uma boa performance no conjunto de treino e não conseguir manter essa performance no reconhecimento de novas observações. Para tal, é necessário poder quantificar a performance destes modelos fora do conjunto de treino.
Funções de Erro
É possível aplicar qualquer um dos métodos de treino anteriormente referidos e, de modo a quantificar o erro num conjunto de treino, é possível estimar uma função de erro, também conhecida por loss function. Estas funções de erro são calculadas no conjunto de teste, e é computada a sua média e desvio padrão em cada um dos folds, no caso de se utilizar validação cruzada.
Algumas medidas de erro são:
- Mean Absolute Error (MAE)
- Root Mean Square Error (RMSE)
- Mean Absolute Percentage Error (MAPE)
Análise de Resíduos
À quantidade dá-se o nome de resíduo (residue). A sua análise, tipicamente através de um scatter plot por cada um dos atributos, pode ser útil para identificar a presença de learning biases, onde existe uma tendência para um padrão ou comportamento particular.
Generalização
Após a tarefa de treino, o modelo deve ser capaz de prever ou descrever novas observações. Se a nova observação pertencer à mesma população, estamos perante uma generalização de primeira ordem. Caso contrário, estamos perante uma generalização de segunda ordem. O objetivo é, então, evitar o underfitting e o overfitting do modelo aos dados de treino. Abaixo encontra-se a definição formal de overfitting.
O processo de aprendizagem num elevado número de dimensões é mais suscetível a overfitting comparativamente a um baixo número de dimensões. Isto deve-se ao facto de, à medida que as dimensões aumentam, a importância de cada uma das componentes diminui, devido ao crescimento do volume com o número de dimensões. Assim, os dados rapidamente se tornam bastante esparsos (com muitos 0's), fazendo com que o modelo sofra de overfitting.
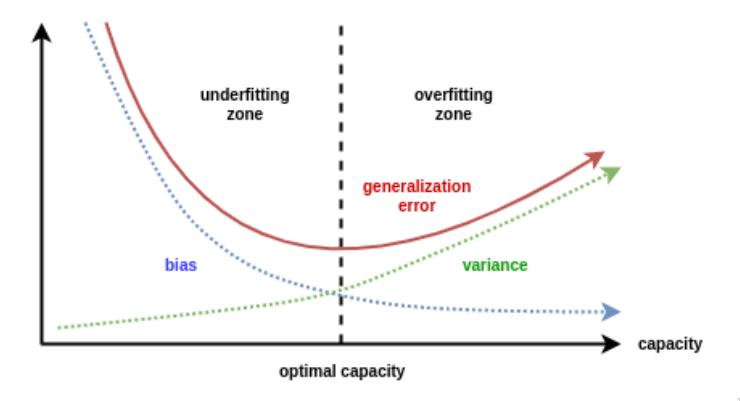
Bias e Variância
É possível demonstrar que o erro é constituído por duas principais componentes, juntamente com alguns termo provenientes do ruído dos dados.
A primeira corresponde a um bias, que reflete a inabilidade do modelo aprendido em aproximar a função geradora (a que melhor se aproxima dos dados). Tal componente pode ter uma elevada contribuição se o modelo não tiver poder expressivo suficiente. É considerado um erro de aproximação.
A segunda componente, a variância, é descrita pela inadequação da informação presente nos dados de treino sobre a função geradora. É considerado um erro de estimação.
Os bons modelos conseguem um balanço entre estas duas componentes. Um modelo com elevado poder expressivo mas com uma amostra de treino limitada consegue um pequeno bias a custo de uma elevada variância, sofrendo de overfitting. Por outro lado, um modelo com baixo poder expressivo consegue uma baixa variância, porém um bias elevado, sofrendo de underfitting.
Para qualquer modelo, apenas conseguimos eliminar o bias e a variância simultaneamente com um conjunto de treino infinito.