Grafos
Definição e Representação
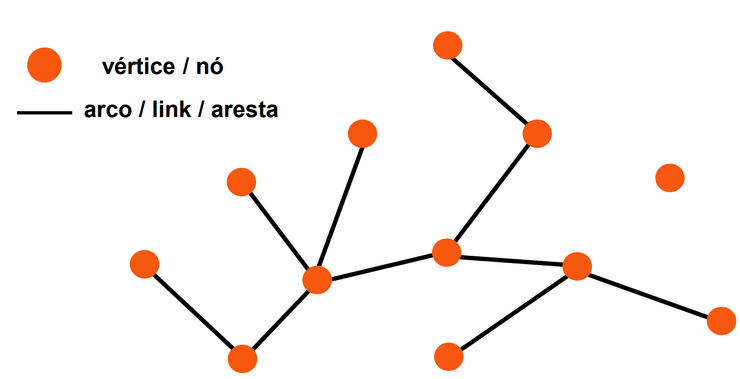
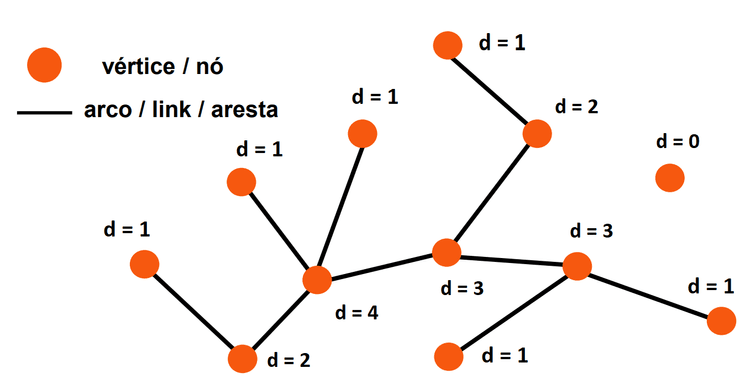
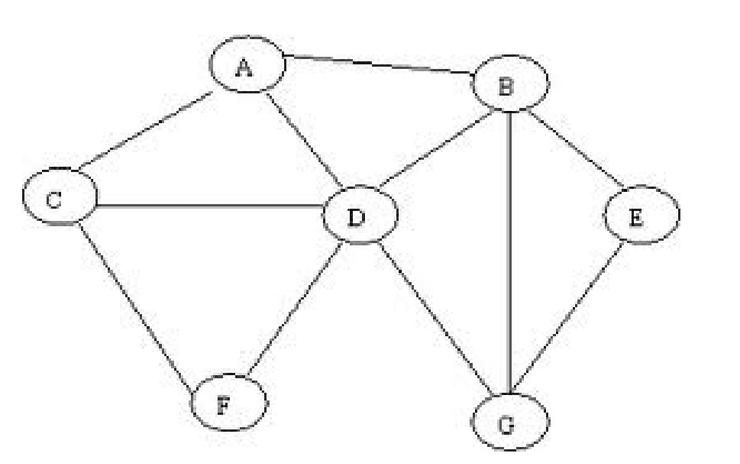
Um grafo corresponde a uma estrutura de dados , com e sendo respetivamente os seus conjuntos de vértices e arestas. Trivialmente, uma aresta (ou arco) liga 2 vértices, e um vértice pode estar ligado a qualquer número de outros vértices. Dizemos que o número de ligações de um vértice é o seu grau, ou degree. Na imagem abaixo podemos observar o grau de cada vértice, :
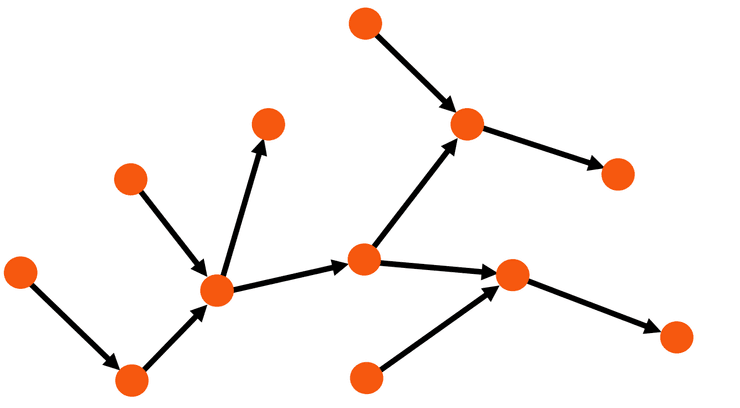
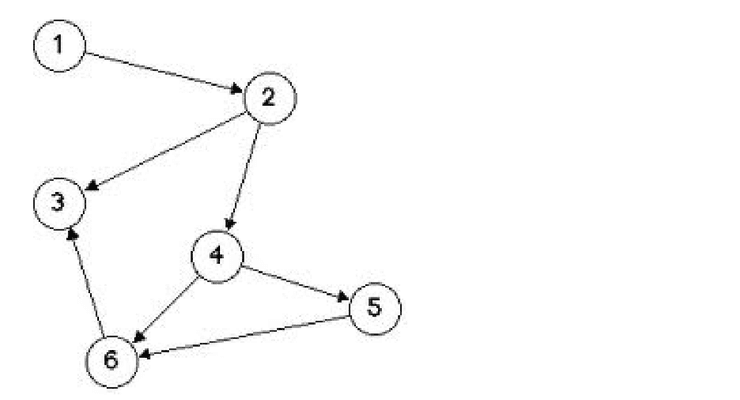
Existem várias tipologias diferentes de grafos. Podemos, por exemplo, querer que as ligações dos vértices tenham uma direção associada: numa fábrica, por exemplo, as linhas de montagem têm por norma sentido único, algo semelhante ao que pretendemos representar aqui. Dizemos que estes grafos são dirigidos ou orientados.
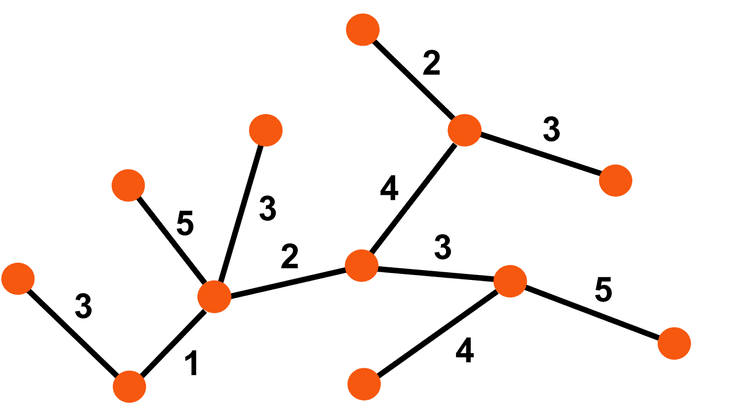
Podemos, claro, pretender pesar as arestas do grafo: pensando numa estrada, caminhos diferentes podem ter custos associados distintos (pensemos, por exemplo, em custos associados a portagens e combustível que variam). Dizemos que estes grafos são pesados.
Em certas situações, podemos querer trabalhar com grafos que não contêm ciclos: isto é, grafos onde partindo de qualquer vértice não encontramos um caminho de volta ao mesmo. Podemos, por exemplo, pensar em circuitos ou redes, onde a existência de ciclos pode (ou não, claro) trazer problemas, preferindo por norma grafos sem ciclos. Dizemos que estes grafos são acíclicos.
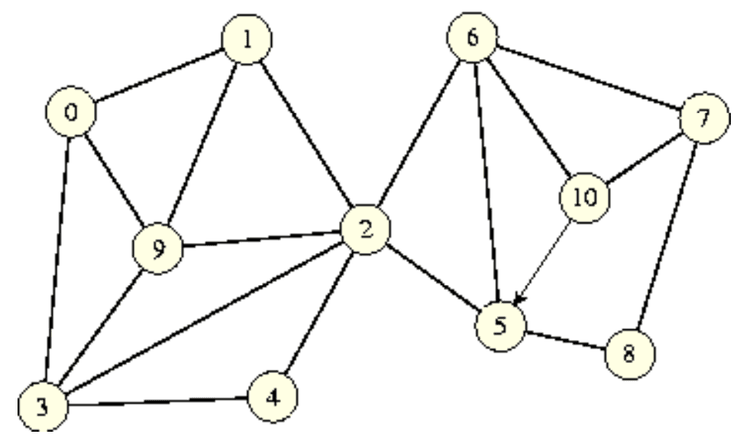
No outro espectro, temos grafos onde, escolhendo qualquer par de vértices do grafo, podemos sempre percorrer um caminho que nos leva de a . Grafos com esta propriedade dizem-se conexos. Podem experimentar verificar esta propriedade a olho no grafo representado abaixo, e notar que a propriedade se verifica!
Temos ainda uma variação adicional dos grafos conexos: os grafos bi-conectados, grafos conexos onde podemos remover qualquer vértice e manter o grafo conexo.
Representação
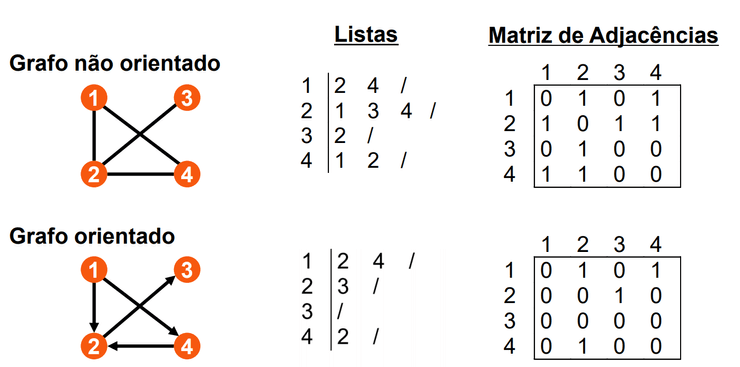
As duas representações mais comuns para grafos (e as abordadas em IAED) são as matrizes de adjacências e as listas de adjacências, cada uma com os respetivos prós e contras. De notar que a própria representação difere entre grafos dirigidos e não dirigidos, como se pode ver na imagem abaixo:
Lista de Adjacências
Nesta representação, cada índice da lista está associado a um vértice do grafo. Esta representação procura, assim, associar a cada vértice um conjunto de vértices , , correspondente aos vértices adjacentes a .
A noção de adjacência difere entre grafos dirigidos e não dirigidos: no caso dos grafos dirigidos, a adjacência é no sentido , ou seja, o vértice que estamos a ver, , é adjacente a outro vértice caso haja um arco dirigido de para . No caso dos grafos não dirigidos, não havendo esta noção de "sentido" associada aos arcos, temos apenas que dois vértices são adjacentes se houver um arco que os ligue.
Vantagens
-
Inicialização é proporcional a , o tamanho do conjunto (ser linear é definitivamente um ponto positivo);
-
Utiliza sempre espaço proporcional a , sendo portanto adequado para grafos esparsos (e em algoritmos que assentem na análise de arcos em grafos esparsos);
-
A adição de arcos é feita de forma eficiente: adicionar um arco de para à lista consiste apenas em fazer um pushback de para o final da lista de , feito em tempo constante.
Desvantagens
-
Verificar arcos paralelos e adjacência entre vértices requer que se pesquise as listas de adjacências, algo que pode levar um tempo proporcional a ;
-
A remoção de arcos pode levar um tempo proporcional a (visto que precisamos de pesquisar o arco em si na lista para o remover);
Não é aconselhável, portanto, para grafos de grande dimensão que não podem ter arcos paralelos (já que, temos de verificar frequentemente se um arco) ou em algoritmos onde esperamos muitas remoções de arcos.
Matriz de Adjacências
Matriz onde as linhas e colunas representam os vértices do grafo. É inicialmente composta totalmente por zeros, representando a ausência de adjacência entre os vértices (linha) e (coluna). Cada vez que encontramos uma nova adjacência, colocamos um na posição correspondente à adjacência na matriz.
Tal como na lista de adjacências, a matriz é preenchida de forma diferente consoante o grafo seja ou não dirigido: no caso de grafos não-dirigidos, havendo uma adjacência entre e no grafo, tanto a entrada como a ficam a ; caso contrário, apenas alteramos o valor da entrada .
Vantagens
A representação é a mais adequada quando temos:
- Bastante espaço disponível (isto é, não são impostas grandes limitações quanto à memória que podemos utilizar);
- Estamos a trabalhar com grafos densos (com muitos arcos, portanto);
- Algoritmos que possam requerer mais de operações.
As afirmações acima advêm da adição e remoção de arcos ser feita de forma eficiente (), de ser fácil evitar existência de arcos paralelos (também verificável em , claro), e de ser igualmente fácil determinar se 2 vértices estão ou não ligados (numa direção ou noutra).
Desvantagens
- Grafos esparsos de grande dimensão requerem espaço de memória proporcional a . Num grafo esparso, grande parte dessa memória acaba por ser inutilizada, acabando por ser uma gestão de recursos pouco sensata;
- Neste caso, apenas inicializar o grafo (tempo proporcional a ) pode dominar o tempo de execução global do algoritmo;
- Para o caso de grafos muito esparsos, mas com um número muito elevado de vértices, podemos nem ter acesso a memória suficiente para armazenar a matriz!
Representações Alternativas
Temos, portanto, três maneiras "básicas" para representar grafos:
- Vector de arcos (pouco comum, não foi abordada em detalhe nesta secção dada a sua simplicidade);
- Matriz de adjacências;
- Lista de adjacências.
Cada uma destas representações, como pudemos observar ao longo da secção, produzem diferentes desempenhos (tanto quanto ao aspeto temporal como espacial) ao nível das respetivas operações de manipulação. A escolha deverá, portanto, depender do problema a resolver.
Algoritmos de Procura em Grafos
Esta sub-secção foi abordada com mais detalhe (e suporte teórico) na secção análoga da página de ASA. Notem que definitivamente não precisam de saber os algoritmos com todo a minúcia teórica apresentada nessa página: para IAED, de um modo geral, costuma bastar saber como o algoritmo funciona/saber executar o algoritmo sobre um grafo arbitrário.