Páscoa

Ciclo de Méton
- Número de Ouro do Calendário
Matriz Lunar
- Sequência dos Números de Ouro
Cálculo da Páscoa
Páscoa Gregoriana

A Páscoa é celebrada no primeiro domingo após a 1ª Lua Cheia, a contar do equinócio da Primavera (que é sempre dia 21 de março).
Se a Lua Cheia calhar num domingo, a Páscoa será no domingo seguinte.

Ciclo de Méton

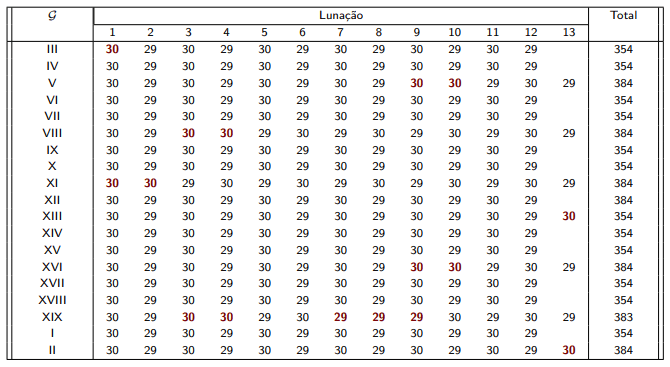
O Ciclo de Méton, descrito em cima, é um ciclo de 19 anos que simula o verdadeiro comportamento da Lua. Um ano pode ter 12 ou 13 ciclos lunares.
Cada mês/ciclo lunar começa e acaba com uma Lua Nova.

Algumas características do Ciclo de Méton:

Meses embolísticos - meses adicionados para corrigir a aproximação (os meses 13);
Saltus lunae - Um dia que é retirado ao ano XIX, ficando com 3 meses de 29 dias seguidos (também para corrigir a aproximação);
Não contempla anos bissextos (a soma dos 19 totais dá $19 \cdot 365$ ) pelo que a longo prazo este ciclo estaria desajustado. Isto foi corrigido pela forma gregoriana como veremos à frente.
O primeiro mês tem sempre 30 dias (mês onde o ciclo lunar começa em dezembro e acaba em janeiro);
O mês Pascal tem sempre 29 dias;
O ano III começa dia 1 de janeiro.

Número de Ouro do Calendário

Para um dado ano $\lambda$ , o seu respetivo ano do Ciclo de Méton é o Número de Ouro.
Seja $G$ o Número de Ouro do ano $\lambda$ ,

G = 1 + \lambda\%19

Lógica da Fórmula

$G$ varia entre 1-19;
O ano 1 a.C. teve Número de Ouro 1

Matriz Lunar

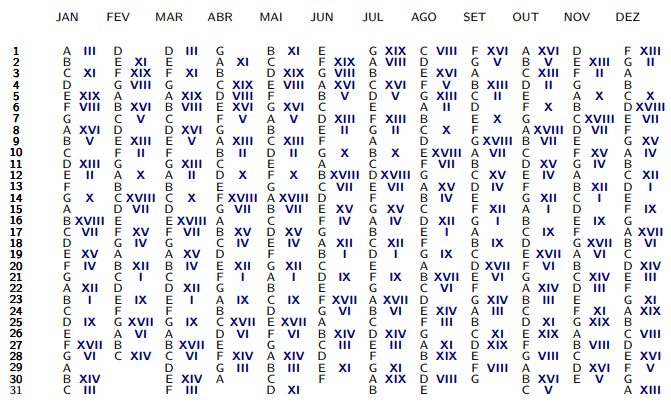
Na Matriz Lunar estão representados os dias de cada ano do Ciclo de Méton que são Lua Nova.
Por exemplo, 2 de fevereiro é Lua Nova no ano XI do Ciclo de Méton.

NOTA

As Luas Cheias são 13 dias depois das Luas Novas

Com a Matriz Lunar conseguimos determinar as datas limite da Páscoa.

Datas Limite da Páscoa

Primeiro Dia

Será quando a Lua Cheia calha o mais cedo possível, a partir do início da Primavera.
Vendo a Matriz Lunar, o Número de Ouro XVI tem uma Lua Nova dia 8 de março, exatamente 13 dias antes do equinócio da Primavera.

Nos anos com Número de Ouro XVI, onde há Lua Cheia no equinócio, se esta calhar a um sábado, a Páscoa será logo no dia 22 de março, a primeira data possível para a Páscoa.

Último dia

Será nos anos onde a Lua Cheia ocorre mesmo antes do dia do equinócio de Primavera.
Olhando para a Matriz Lunar, conclui-se que será nos anos com Número de Ouro VIII, que têm uma Lua Cheia no dia 19 de março.
Recorrendo à tabela mais uma vez, repara-se que a Lua Cheia seguinte será dia 18 de abril (já que há uma Lua Nova dia 5 de abril).

Nestes anos, se a Lua Cheia calhar num domingo, a Páscoa será no domingo seguinte (+7 dias), ou seja, no dia 25 de abril, a última data possível para a Pascoa.

Sequência dos Números de Ouro

Seja $G_n$ o n-ésimo Número de Ouro representado na Matriz Lunar,

G_1 = 3\\ G_n = (G_{n-1}+8)\%19

Exemplos

G_2 = (G_1+8)\%19\\ = (3+8) = 11 \checkmark

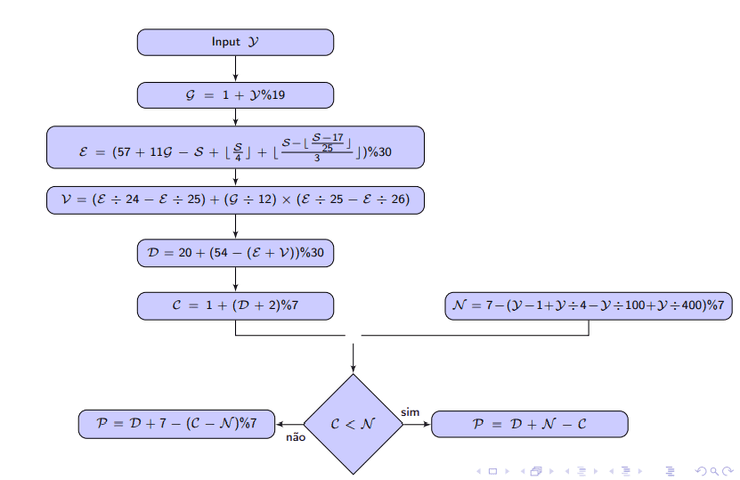
Cálculo da Páscoa

Epacta

Há quantos dias foi a última Lua Nova, relativamente ao dia 1 de janeiro.

A Epacta é um número de 0-29, que pode ser dado por:

E = (8 +11(G -1))\% 30\\ G \rightarrow \text{número de ouro}

Lógica da Fórmula

A Epacta pode ser vista como o "atraso" dos anos lunares, em relação aos anos solares (anos de 365 dias, anos bissextos serão contemplados depois);
Aumenta 11 dias por ano (diferença entre ano solar e lunar);
Anos com meses embolísticos ocorrem sempre quando os anos lunares estam atrasados $d \geq 30$ dias, em comparação com anos solares. Estes anos adicionam 30 dias ao calendário lunar, que diminuem o atraso (Epacta);
*(Exemplo no fim)
Epacta do Número de Ouro I é 8, onde já é aplicada a correção em relação ao saltus lunae (ano XIX tem menos 1 dia que os restantes).

Logo,

E = (8 +11(G -1))\% 30

*Exemplo:

Sabe-se que a Epacta do ano III é $0$ , logo será $11$ e $22$ nos anos IV e V. Como o ano V é um ano com mês embolístico, a Epacta/atraso face aos anos solares do próximo ano vai ser menor (-30).

E_{VI} = 11 + 11 + 11 - 30\\ =3

Esta relação é mantida para todos os Números de Ouro.

Teorema 1 - Simplificação da Fórmula

É possível calcular a epacta somente através de:

E = (11G -3)\% 30

Demonstração

E = (8 +11(G -1))\% 30\\ E=(8+11G-11)\% 30\\ E=(11G-3)\%30

QED

Teorema 2 - Unicidade da Epacta

Existe um único valor da Epacta para cada ano do Ciclo de Méton.

Lua Cheia Pascal

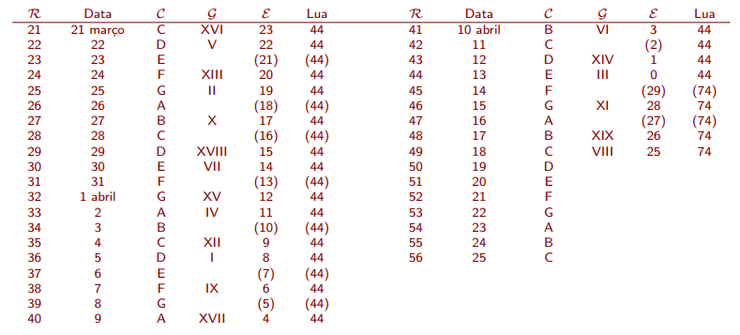
O dia, a partir de 21 de março, da Lua Cheia que determina o domingo de Páscoa pode ser dado por:

R = \begin{cases} 44 - E,\qquad E < 24 \\ 74-E,\qquad E \geq 24 \end{cases}

Note-se que há casos onde $R>31$ , e março tem apenas 31 dias. Isto acontece, pois os dias de abril são considerados dias de março, ou seja, 1 de abril é dia 32 de março e 10 de abril é dia 41 de março, por exemplo.

Lógica da Fórmula

Uma propriedade interessante é que a soma da Epacta, de um ano $\lambda$ ,com o dia do mês de março $(R)$ onde calha a Lua Cheia Pascal, contando os dias de abril como continuação do mês de março, é:

$44, \quad$ entre 21 e 44 de março (13 de abril)
$74, \quad$ entre 45 e 49 de março (18 de abril, última data possível para a Lua Cheia Pascal)

NOTA: As Luas Cheias são 13 dias depois da Lua Nova. Conseguimos obter todas as Luas Cheias, de cada Número de Ouro, através da Tabela das Luas Novas.

Desta forma, é simples chegar à fórmula apresentada.

Teorema 3 - Simplificação da fórmula

R = 20 + (54-E)\% 30\\ E \rightarrow \text{Epacta}

Demonstração

Se $E \geq 24$ :

R = 74 - E\\ =20 + 54 - E\\ = 20 + (54-E)\% 30

Se $E < 24$ :

R = 44 - E\\ =20 + 24 - E\\ = 20 + (24-E)\% 30\\ = 20 + (54-E)\% 30

Exemplo - Páscoa Juliana

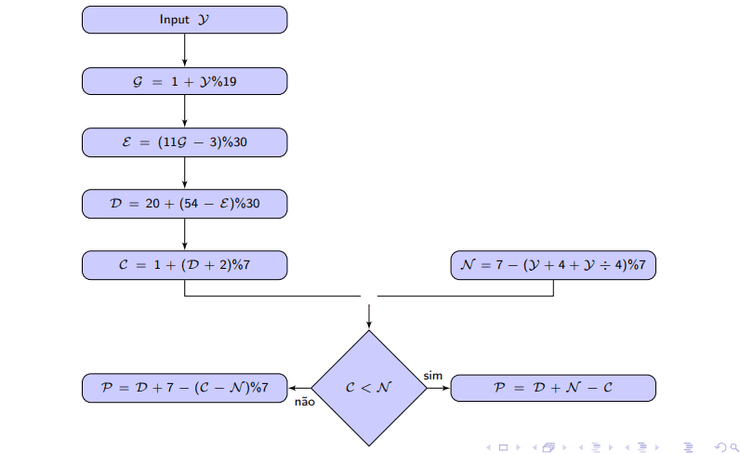
Agora que já sabemos a data da Lua Cheia Pascal, basta determinar quando é o primeiro domingo que vem depois desta. O número de dias que falta para domingo é determinado pelo número calêndrico de um dia e pelo número dominical do ano, nomeadamente, pela quantidade $N-C$ .

Exemplo

Calcular o dia da Páscoa para o ano 1901.

Número Dominical ( $N$ )

N = 7 - (1901 + 4 + (1901\div 4))\% 7\\ = 7 - (2380)\% 7 = 7

Número de Ouro ( $G$ )

G = 1 + (1901)\%19=1+1=2

Epacta ( $E$ )

E = (11G-3)\%30 \\ = (11(2)-3)\%30 = 19

Dia da Lua Cheia Pascal ( $R$ )

R = 20 + (54 - E)\%30\\ = 20 +5 = 25

Número Calêndrico da Lua Cheia Pascal ( $C$ )

C = 1 + (R+2)\%7\\ = 1 + 6 = 7

Dia da Páscoa

Como $N \leq C$ ,

P = R + 7 - (C-N)\%7\\ =25 +7 -0 = 32

Dia "32 de março", ou seja, dia 1 de abril.

NOTA IMPORTANTE

Se $N>C$ ,

P= D + N - C

Páscoa Gregoriana

A Reforma Gregoriana trouxe novas regras com consequências no Cálculo da Páscoa.

Foram retirados 10 dias ao Calendário no ano 1582
A partir do ano 1600, de 100 em 100 anos deixou e haver ano bissexto, voltando a acontecer de 400 em 400 anos.
A partir de 1800, começou-se a tirar um dia à Lua de 300 em 300 anos, com um exceção no 8º dia a retirar, que tem um intervalo de 400 anos. (A primeira ocorrência não conta)

Epacta Gregoriana

Os 10 dias retirados ao Calendário no ano 1582 e as novas regras associadas aos anos bissextos e à Lua levaram à adição de 2 correções na fórmula da Epacta. Seja $E_G$ a Epacta Gregoriana, é dada por:

$E_G = (11(G-3) -($ Correção de 1582 $)-($ Correção após 1582 $))\% 30$

Correção de 1582

Esta correção e diz respeito aos 10 dias retirados ao Sol e os 4 dias retirados à Lua no Calendário Gregoriano em 1582. É uma correção muito simples, uma vez que foi pontual.
Esta correção, $C_1$ , é dada por:

C_1 = 6 +1\\ 6 \rightarrow \text{diferença entre a correção do Sol e a correção da Lua}\\ (10 - 4 = 6)\\ 1 \rightarrow \text{Convenção para que a Páscoa Gregoriana seja}\\ \text{sempre diferente da Páscoa Judaica}

Correção após 1582

Esta correção tem por base os dias adicionados ao Sol e os dias retirados à Lua, ao longo dos anos.

NOTA

Em aritmética do Calendário define-se século ( $S$ ), como os primeiros $n-2$ dígitos de uma ano ( $n$ é u número de dígitos do ano). Por exemplo,

S_{2020} = 20 \quad S_{12345}=123 \quad S_{12}=0

Equação do Sol

Corrige os dias descontados ao Calendário Gregoriano, que são adicionados no Calendário Juliano. Mais especificamente, desconta os dias dos anos de 100 em 100, porque não são bissextos (com a exceção do ano bissexto de 400 em 400 anos).
Sendo $E_{sol}$ a equação do Sol, é dada por:

E_{sol}=3 \times((S-16)\div 4)+(S-16)\%4\\ 3 \times((S-16)\div 4) \rightarrow \text{De 400 em 400 ano são descontados 3 dias}\\ (S-16)\%4 \rightarrow \text{Até chegar ao fim do ciclo de 400 anos,}\\ \text{ desconta-se 1 dia em cada 100 anos}

Exemplo

Equação do Sol para o ano 2233
$S = 22$

E_{sol} = 3 \times((22-16)\div 4)+(22-16)\%4\\ = 3+2 = 5\\ 3 \rightarrow \text{Dias descontados dos 3 anos não bissextos (de 100 em 100) entre 1600 e 1900}\\ 2 \rightarrow \text{Dias descontados em 2100 e 2200}

É possível simplificar esta equação, ficando esta da seguinte forma:

E_{sol} = S - (S\div4)-12

Equação da Lua

Vendo a Tabela do Sol e Lua, nota-se que a regularidade da Lua ocorre de 25 em 25 séculos e, em cada ciclo de 25, retiramos 8 dias à Lua. Seja $E_{lua}$ a Equação da Lua, esta é dada por:

Z= (S-18)\%25\\ E_{lua} = 1 + (8 \times((S-18)\div25) + (Z\div 3)- (Z\div 24)\\~\\ 1 \rightarrow \text{Dia omitido em 1800}\\ (8 \times((S-18)\div25) \rightarrow \text{8 dias em cada 25 séculos}\\ (Z\div 3)- (Z\div 24) \rightarrow \text{dias omitidos}\\\text{antes de se completar o ciclo de 25 séculos}

Repare-se que $Z$ é o número de séculos do ciclo de 25 séculos a analisar. De 300 em 300 anos é retirado um dia à Lua, mas no 24º século não (a exceção).
Deste modo, quando $Z < 24$ , $(Z\div 24)=0$ e $(Z \div 3)$ devolve os dias a descontar. Para $Z=24$ é preciso adicionar o dia que é retirado indevidamente pelo $(Z \div 3)$ , e é por isso que está lá o $(Z\div 24)$ .

NOTA

Estamos a calcular os dias que vão ser omitidos, por isso é que se tem $- (Z\div24)$ . Ao adicionar um dia, está a retirar um dia aos omitidos

Simplificando a Equação da Lua, ficamos com:

E_{lua} = \left\lfloor\frac{S-\left\lfloor\frac{S-17}{25}\right\rfloor}{3}\right\rfloor

Finalmente, podemos chegar à Equação que nos dá a Correção após 1582 ( $C_2$ ).

C_2 = E_{sol}- E_{lua}\\ = S - (S\div4)-12- \left\lfloor\frac{S-\lfloor\frac{S-17}{25}\rfloor}{3}\right\rfloor

NOTA

$\lfloor\frac a b\rfloor$ é equivalente a $a\div b$ (divisão inteira)

Conclusão

A Epacta Gregoriana é dada por:

E_G = (11(G-3) -C_1-C_2)\% 30\\ = (11(G-3) -(6+1)-(S - (S\div4)-12- \left\lfloor\frac{S-\left\lfloor\frac{S-17}{25}\right\rfloor}{3}\right\rfloor)\% 30

Simplificando

E_G=\left(57+11G-S+(S\div4) + \left\lfloor\frac{S-\left\lfloor\frac{S-17}{25}\right\rfloor}{3}\right\rfloor\right)\% 30

Correção de Clavius

Uma das Regras Base da Páscoa, que foi mantida na Reforma Gregoriana, é que as Luas Novas que irão determinar a Páscoa estão compreendidas entre 8 de março e 5 de abril.
Com as alterações da Epacta, há casos onde isto já não acontece.
Com a Correção de Clavius ( $V$ ), isto é corrigido.