O seguinte vídeo apresenta contexto histórico e uma pequena intuição do algoritmo:
VIDEO
Daqui em diante define-se polinómio p : C → C p:\mathbb{C}\to\mathbb{C} p : C → C r − 1 r-1 r − 1
p ( c ) = a 0 + a 1 c + a 2 c 2 + a 3 c 3 + a 4 c 4 + ⋯ + a r − 1 c r − 1 p(c)=a_0+a_1c+a_2c^2+a_3c^3+a_4c^4+\dots+a_{r-1}c^{r-1} p ( c ) = a 0 + a 1 c + a 2 c 2 + a 3 c 3 + a 4 c 4 + ⋯ + a r − 1 c r − 1 Agora, tomando λ 0 , λ 1 , λ 2 , … , λ r − 1 ∈ C \lambda_0, \lambda_1, \lambda_2,\dots, \lambda_{r-1} \in \mathbb{C} λ 0 , λ 1 , λ 2 , … , λ r − 1 ∈ C
p ( λ 0 ) = a 0 + a 1 λ 0 + a 2 λ 0 2 + a 3 λ 0 3 + ⋯ + a r − 1 λ 0 r − 1 p ( λ 1 ) = a 0 + a 1 λ 1 + a 2 λ 1 2 + a 3 λ 1 3 + ⋯ + a r − 1 λ 1 r − 1 p ( λ 2 ) = a 0 + a 1 λ 2 + a 2 λ 2 2 + a 3 λ 2 3 + ⋯ + a r − 1 λ 2 r − 1 ⋮ p ( λ r − 1 ) = a 0 + a 1 λ r − 1 + a 2 λ r − 1 2 + a 3 λ r − 1 3 + ⋯ + a r − 1 λ r − 1 r − 1 p(\lambda_0)=a_0+a_1\lambda_0+a_2\lambda_0^2+a_3\lambda_0^3+\dots+a_{r-1}\lambda_0^{r-1}\\
p(\lambda_1)=a_0+a_1\lambda_1+a_2\lambda_1^2+a_3\lambda_1^3+\dots+a_{r-1}\lambda_1^{r-1}\\
p(\lambda_2)=a_0+a_1\lambda_2+a_2\lambda_2^2+a_3\lambda_2^3+\dots+a_{r-1}\lambda_2^{r-1}\\
\vdots\\
p(\lambda_{r-1})=a_0+a_1\lambda_{r-1}+a_2\lambda_{r-1}^2+a_3\lambda_{r-1}^3+\dots+a_{r-1}\lambda_{r-1}^{r-1} p ( λ 0 ) = a 0 + a 1 λ 0 + a 2 λ 0 2 + a 3 λ 0 3 + ⋯ + a r − 1 λ 0 r − 1 p ( λ 1 ) = a 0 + a 1 λ 1 + a 2 λ 1 2 + a 3 λ 1 3 + ⋯ + a r − 1 λ 1 r − 1 p ( λ 2 ) = a 0 + a 1 λ 2 + a 2 λ 2 2 + a 3 λ 2 3 + ⋯ + a r − 1 λ 2 r − 1 ⋮ p ( λ r − 1 ) = a 0 + a 1 λ r − 1 + a 2 λ r − 1 2 + a 3 λ r − 1 3 + ⋯ + a r − 1 λ r − 1 r − 1 Igualdades estas que podem ser representadas matricialmente:
[ p ( λ 0 ) p ( λ 1 ) p ( λ 2 ) … p ( λ r − 1 ) ] = [ a 0 a 1 a 2 … a r − 1 ] ⋅ V r \begin{bmatrix}p(\lambda_0) & p(\lambda_1) & p(\lambda_2) &\dots & p(\lambda_{r-1})\end{bmatrix} =
\begin{bmatrix}a_0& a_1 & a_2 & \dots & a_{r-1}\end{bmatrix}\cdot V_r [ p ( λ 0 ) p ( λ 1 ) p ( λ 2 ) … p ( λ r − 1 ) ] = [ a 0 a 1 a 2 … a r − 1 ] ⋅ V r Onde V r V_r V r matriz de Vandermonde devem ser preenchidas com as potências dos respetivos valores de λ \lambda λ
Matriz de Vandermonde = [ λ 0 0 λ 0 1 λ 0 2 … λ 0 r − 1 λ 1 0 λ 1 1 λ 1 2 … λ 1 r − 1 λ 2 0 λ 2 1 λ 2 2 … λ 2 r − 1 … … … … … λ r − 1 0 λ r − 1 1 λ r − 1 2 … λ r − 1 r − 1 ] \text{Matriz de Vandermonde} = \begin{bmatrix} \lambda_0^0 & \lambda_0^1 & \lambda_0^2 & \dots & \lambda_0^{r-1} \\
\lambda_1^0 & \lambda_1^1 & \lambda_1^2 & \dots &\lambda_1^{r-1} \\
\lambda_2^0 & \lambda_2^1 & \lambda_2^2 & \dots &\lambda_2^{r-1} \\
\dots & \dots & \dots & \dots & \dots \\
\lambda_{r-1}^0 & \lambda_{r-1}^1 & \lambda_{r-1}^2 & \dots &\lambda_{r-1}^{r-1} \\
\end{bmatrix} Matriz de Vandermonde = λ 0 0 λ 1 0 λ 2 0 … λ r − 1 0 λ 0 1 λ 1 1 λ 2 1 … λ r − 1 1 λ 0 2 λ 1 2 λ 2 2 … λ r − 1 2 … … … … … λ 0 r − 1 λ 1 r − 1 λ 2 r − 1 … λ r − 1 r − 1 Chamando então à matriz à esquerda da igualdade Y Y Y V r V_r V r X X X
Y T = X T V r Y^T= X^TV_r Y T = X T V r É de notar que a matriz de Vandermonde tem inversa! Assim, é possível chegar aos coeficientes de um polinómio a partir dos seus valores, e vice-versa. Neste problema, a escolha dos valores para os λ ′ s \lambda's λ ′ s r r r Porquê? Utilizando estes valores, as contas são imensamente facilitadas, principalmente devido à consequente simetria da matriz de Vandermonde.
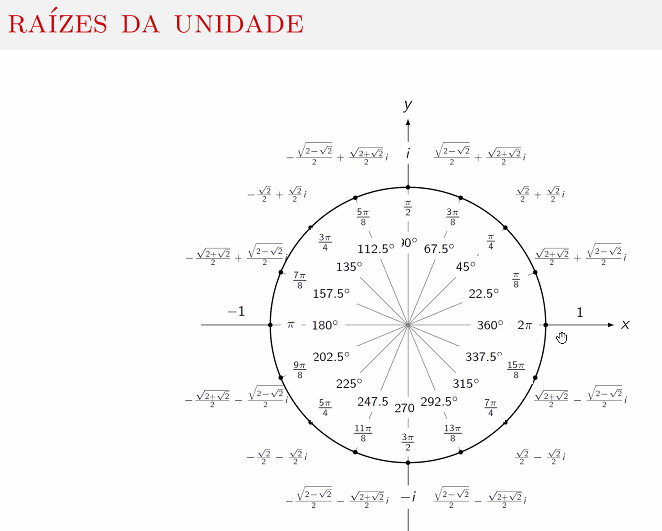
Chamam-se a w 0 , w 1 , w 2 , w 3 , … , w r − 1 , w r ( = 1 ) w^0, w^1, w^2, w^3,\dots, w^{r-1}, w^r(=1) w 0 , w 1 , w 2 , w 3 , … , w r − 1 , w r ( = 1 ) raiz principal pode ser obtida através da fórmula:
w = e i 2 π r = cis ( 2 π r ) = cos ( 2 π r ) + i sin ( 2 π r ) w=e^{i\frac{2\pi} r}=\operatorname{cis}\left(\frac{2\pi} r\right) = \cos\left(\frac {2\pi}{r}\right)+i\sin\left(\frac{2\pi} r\right) w = e i r 2 π = cis ( r 2 π ) = cos ( r 2 π ) + i sin ( r 2 π ) Para r = 16 r=16 r = 16
Assim, utilizando esta notação, a matriz de Vandermonde viria:
[ 1 w 0 w 0 2 w 0 3 … w 0 r − 1 1 w 1 w 1 2 w 1 3 … w 1 r − 1 1 w 2 w 2 2 w 2 3 … w 2 r − 1 … … … … … … 1 w r − 1 w r − 1 2 w r − 1 3 … w r − 1 r − 1 ] \begin{bmatrix} 1 & w_0 & w_0^2 & w_0^3 & \dots & w_{0}^{r-1}\\ 1 & w_1 & w_1^2 & w_1^3 & \dots & w_{1}^{r-1}\\ 1 & w_2 & w_2^2 & w_2^3 & \dots & w_{2}^{r-1}\\ \dots & \dots & \dots & \dots & \dots &\dots \\ 1 & w_{r-1} & w_{r-1}^2 & w_{r-1}^3 & \dots & w_{r-1}^{r-1}\end{bmatrix} 1 1 1 … 1 w 0 w 1 w 2 … w r − 1 w 0 2 w 1 2 w 2 2 … w r − 1 2 w 0 3 w 1 3 w 2 3 … w r − 1 3 … … … … … w 0 r − 1 w 1 r − 1 w 2 r − 1 … w r − 1 r − 1 ou seja, a raiz de Vandermonde para as raízes de índice 4 da unidade viria:
V 4 = [ 1 1 1 1 1 i − 1 − i 1 − 1 1 − 1 1 − i − 1 i ] V_4=\begin{bmatrix} 1 & 1 & 1 & 1
\\ 1 & i & -1 & -i\\1 & -1 & 1 & -1 \\ 1 & -i & -1 & i\end{bmatrix} V 4 = 1 1 1 1 1 i − 1 − i 1 − 1 1 − 1 1 − i − 1 i Repara-se que, aproveitando-se da simetria nestes casos:
X T = Y T V r − 1 ⇔ X = ( V r T ) − 1 Y = V r − 1 Y X^T= Y^T V_r^{-1} \Leftrightarrow X=(V_r^T)^{-1}Y = V_r^{-1}Y X T = Y T V r − 1 ⇔ X = ( V r T ) − 1 Y = V r − 1 Y tomando agora proveito da progressão geométrica, vem:
ρ r − 1 ρ − 1 = 1 + ρ + ρ 2 + ⋯ + ρ r − 1 ⇔ ( ρ r − 1 ) = ( ρ − 1 ) ( 1 + ρ + ρ 2 + ⋯ + ρ r − 1 ) ⇔ Sabendo que ρ r = 1 , vem: ρ = 1 ou 1 + ρ + ρ 2 + ⋯ + ρ r − 1 = 0 \frac{\rho^r-1}{\rho-1} = 1+\rho+\rho^2+\dots+\rho^{r-1} \Leftrightarrow\\
(\rho^r-1)=(\rho-1)(1+\rho+\rho^2+\dots+\rho^{r-1})\Leftrightarrow \\\text{Sabendo que }\rho^r=1, \text{ vem:} \\
\rho=1\quad \text{ou}\quad 1+\rho+\rho^2+\dots+\rho^{r-1}=0 ρ − 1 ρ r − 1 = 1 + ρ + ρ 2 + ⋯ + ρ r − 1 ⇔ ( ρ r − 1 ) = ( ρ − 1 ) ( 1 + ρ + ρ 2 + ⋯ + ρ r − 1 ) ⇔ Sabendo que ρ r = 1 , vem: ρ = 1 ou 1 + ρ + ρ 2 + ⋯ + ρ r − 1 = 0 Como a raiz principal nunca é 1, descobrimos que a soma de todas as raízes de índice r r r
Tome-se então, a multiplicação entre uma linha de uma matriz de Vandermonde com uma coluna de uma outra matriz de Vandermonde, vem:
[ 1 w k w 2 k w 3 k … w ( r − 1 ) k ] ⋅ [ 1 w − j w − 2 j w − 3 j ⋮ w − ( r − 1 ) j ] = 1 + w k − j + w 2 ( k − j ) + w 3 ( k − j ) + ⋯ + w ( r − 1 ) ( k − j ) \begin{bmatrix} 1 & w^k & w^{2k} & w^{3k} & \dots & w^{(r-1)k}\end{bmatrix} \cdot \begin{bmatrix} 1 \\ w^{-j} \\ w^{-2j} \\ w^{-3j} \\ \vdots \\ w^{-{(r-1)}j}\end{bmatrix} = \\ 1+w^{k-j} + w^{2(k-j)} + w^{3(k-j)} + \dots + w^{(r-1)(k-j)} [ 1 w k w 2 k w 3 k … w ( r − 1 ) k ] ⋅ 1 w − j w − 2 j w − 3 j ⋮ w − ( r − 1 ) j = 1 + w k − j + w 2 ( k − j ) + w 3 ( k − j ) + ⋯ + w ( r − 1 ) ( k − j ) É de notar que, apesar de w w w w w w
Agora, expandindo este pensamento para matrizes em vez de colunas/linhas, percebe-se que o resultado será uma matriz preenchida por r r r k = j k=j k = j
V r ⋅ V r † = r I n ⇔ V r − 1 = 1 r V r † V_r \cdot V_r^\dagger = rI_n \Leftrightarrow V_r^{-1} = \frac 1 r V_r^\dagger V r ⋅ V r † = r I n ⇔ V r − 1 = r 1 V r † Onde V r † V_r^\dagger V r † V r V_r V r
Ou seja,
X = 1 r V r ( w ) † Y X=\frac 1 r V_r(w)^\dagger Y X = r 1 V r ( w ) † Y Para mais sobre as utilidades da matriz de Vandermonde, podem ver este vídeo.
Antes de passar à multiplicação de polinómios pela FFT , é necessário introduzir alguns conceitos essenciais que levaram à descoberta deste algoritmo.
Rev k : { 0 , 1 } k → { 0 , 1 } k \operatorname{Rev}_k : \{0,1\}^k \rightarrow \{0,1\}^k Rev k : { 0 , 1 } k → { 0 , 1 } k Consiste em transformar uma palavra binária, de k k k simétrica.
Exemplos
Seja k = 4 k = 4 k = 4 Rev 4 ( 1010 ) = 0101 \operatorname{Rev}_4(1010) = 0101 Rev 4 ( 1010 ) = 0101
Seja k = 3 k = 3 k = 3 Rev 3 ( 101 ) = 101 \operatorname{Rev}_3(101) = 101 Rev 3 ( 101 ) = 101
É como colocar um "espelho" no final da palavra. O resultado é a sua reflexão,
n 0 n 1 … n k − 1 ∣ n k − 1 … n 1 n 0 n_0n_1 \dots n_{k-1}\ |\ n_{k-1}\dots n_1n_0 n 0 n 1 … n k − 1 ∣ n k − 1 … n 1 n 0 Também se pode aplicar Rev k \operatorname{Rev}_k Rev k 2 k 2^k 2 k 2 2 × 2 2 2^2\times2^2 2 2 × 2 2
Rev 2 { [ a 0 , 0 a 0 , 1 a 0 , 2 a 0 , 3 a 1 , 0 a 1 , 1 a 1 , 2 a 1 , 3 a 2 , 0 a 2 , 1 a 2 , 2 a 2 , 3 a 3 , 0 a 3 , 1 a 3 , 2 a 3 , 3 ] } = = Rev 2 { [ a 0 , 00 a 0 , 01 a 0 , 10 a 0 , 11 a 1 , 00 a 1 , 01 a 1 , 10 a 1 , 11 a 2 , 00 a 2 , 01 a 2 , 10 a 2 , 11 a 3 , 00 a 3 , 01 a 3 , 10 a 3 , 11 ] } = [ a 0 , 00 a 0 , 10 a 0 , 01 a 0 , 11 a 1 , 00 a 1 , 10 a 1 , 01 a 1 , 11 a 2 , 00 a 2 , 10 a 2 , 01 a 2 , 11 a 3 , 00 a 3 , 10 a 3 , 01 a 3 , 11 ] \operatorname{Rev}_2\left\{\begin{bmatrix}a_{0,0} & a_{0,1} & a_{0,2} & a_{0,3} \\ a_{1,0} & a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,0} & a_{2,1} & a_{2,2} & a_{2,3} \\ a_{3,0} & a_{3,1} & a_{3,2} & a_{3,3} \\\end{bmatrix}\right\} =
\\ = \operatorname{Rev}_2\left\{\begin{bmatrix}a_{0,00} & a_{0,01} & a_{0,10} & a_{0,11} \\ a_{1,00} & a_{1,01} & a_{1,10} & a_{1,11} \\ a_{2,00} & a_{2,01} & a_{2,10} & a_{2,11} \\ a_{3,00} & a_{3,01} & a_{3,10} & a_{3,11} \\\end{bmatrix}\right\} \\ = \begin{bmatrix}a_{0,00} & a_{0,10} & a_{0,01} & a_{0,11} \\ a_{1,00} & a_{1,10} & a_{1,01} & a_{1,11} \\ a_{2,00} & a_{2,10} & a_{2,01} & a_{2,11} \\ a_{3,00} & a_{3,10} & a_{3,01} & a_{3,11} \\\end{bmatrix} Rev 2 ⎩ ⎨ ⎧ a 0 , 0 a 1 , 0 a 2 , 0 a 3 , 0 a 0 , 1 a 1 , 1 a 2 , 1 a 3 , 1 a 0 , 2 a 1 , 2 a 2 , 2 a 3 , 2 a 0 , 3 a 1 , 3 a 2 , 3 a 3 , 3 ⎭ ⎬ ⎫ = = Rev 2 ⎩ ⎨ ⎧ a 0 , 00 a 1 , 00 a 2 , 00 a 3 , 00 a 0 , 01 a 1 , 01 a 2 , 01 a 3 , 01 a 0 , 10 a 1 , 10 a 2 , 10 a 3 , 10 a 0 , 11 a 1 , 11 a 2 , 11 a 3 , 11 ⎭ ⎬ ⎫ = a 0 , 00 a 1 , 00 a 2 , 00 a 3 , 00 a 0 , 10 a 1 , 10 a 2 , 10 a 3 , 10 a 0 , 01 a 1 , 01 a 2 , 01 a 3 , 01 a 0 , 11 a 1 , 11 a 2 , 11 a 3 , 11 Note-se que a Reversão é apenas aplicada aos índices das colunas.2 2 × 2 2 2^2\times2^2 2 2 × 2 2 n × 2 2 n\times 2^2 n × 2 2 n ≥ 1 n\geq 1 n ≥ 1
Seja P k P_k P k I k I_k I k 2 k × 2 k 2^k\times 2^k 2 k × 2 k
P k = Rev k { I k } e P k 2 = P k P k = I k P_k = \operatorname{Rev}_k\{I_k\} \\
\text{e} \\ P_k^2 = P_kP_k = I_k P k = Rev k { I k } e P k 2 = P k P k = I k Exemplos P 2 = Rev 2 { [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ] } ⇔ P 2 = [ 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 ] P_2 = \operatorname{Rev}_2\left\{\begin{bmatrix}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{bmatrix}\right\} \Leftrightarrow \\ P_2 = \begin{bmatrix}1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1\end{bmatrix} P 2 = Rev 2 ⎩ ⎨ ⎧ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ⎭ ⎬ ⎫ ⇔ P 2 = 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 D k = [ w 0 0 0 … 0 0 w 1 0 … 0 0 0 w 2 … 0 … … … … … 0 0 0 … w 2 k − 1 ] D_k = \begin{bmatrix} w_0 & 0 & 0 & \dots & 0
\\ 0 & w_1 & 0 &\dots & 0 \\ 0 & 0 & w_2 & \dots & 0 \\\dots & \dots & \dots & \dots & \dots \\ 0 & 0 & 0 & \dots & w_{2^k-1}\end{bmatrix} D k = w 0 0 0 … 0 0 w 1 0 … 0 0 0 w 2 … 0 … … … … … 0 0 0 … w 2 k − 1 Representada por D k D_k D k 2 k × 2 k 2^k \times 2^k 2 k × 2 k 2 k 2^k 2 k 2 k + 1 2^{k+1} 2 k + 1
Exemplo
Sendo k = 2 k=2 k = 2 2 2 2^2 2 2 2 3 2^3 2 3
e 0 i ⋅ 2 π 2 3 = 1 , e 1 i ⋅ 2 π 2 3 = 2 2 + i 2 2 , e 2 i ⋅ 2 π 2 3 = i , e 3 i ⋅ 2 π 2 3 = − 2 2 + i 2 2 e^{0i\cdot\frac{2\pi}{2^3}} = 1 ,\quad e^{1i\cdot\frac{2\pi}{2^3}} = \frac{\sqrt{2}}{2} + i\frac{\sqrt{2}}{2},\quad e^{2i\cdot\frac{2\pi}{2^3}} = i,\quad e^{3i\cdot\frac{2\pi}{2^3}} = -\frac{\sqrt{2}}{2} + i\frac{\sqrt{2}}{2} e 0 i ⋅ 2 3 2 π = 1 , e 1 i ⋅ 2 3 2 π = 2 2 + i 2 2 , e 2 i ⋅ 2 3 2 π = i , e 3 i ⋅ 2 3 2 π = − 2 2 + i 2 2 logo
D 2 = [ 1 0 0 0 0 2 2 + i 2 2 0 0 0 0 i 0 0 0 0 − 2 2 + i 2 2 ] D_2 = \begin{bmatrix} 1 & 0 & 0 & 0
\\ 0 & \frac{\sqrt{2}}{2} + i\frac{\sqrt{2}}{2} & 0 & 0 \\ 0 & 0 & i & 0 \\ 0 & 0 & 0 & -\frac{\sqrt{2}}{2} + i\frac{\sqrt{2}}{2}\end{bmatrix} D 2 = 1 0 0 0 0 2 2 + i 2 2 0 0 0 0 i 0 0 0 0 − 2 2 + i 2 2 F k ( w ) F_k(w) F k ( w ) 2 k × 2 k 2^k\times2^k 2 k × 2 k
F k ( w ) = ν k ( w ) ⋅ P k F_k(w) = \nu_k(w) \cdot P_k F k ( w ) = ν k ( w ) ⋅ P k onde
w w w w = e i 2 π 2 k = cos ( 2 π 2 k ) + i sin ( 2 π 2 k ) w = e^{i\frac{2\pi}{2^k}} = \cos\left(\frac {2\pi}{2^k}\right)+i\sin\left(\frac{2\pi} {2^k}\right) w = e i 2 k 2 π = cos ( 2 k 2 π ) + i sin ( 2 k 2 π ) P k P_k P k Matriz de Permutação de ordem k k k ν k ( w ) \nu_k(w) ν k ( w ) Matriz de Vandermonde V r ( w ) V_r(w) V r ( w ) 2 k = r 2^k=r 2 k = r
Em suma, é o produto da Matriz de Permutação pela Matriz de Vandermonde.
Define-se, agora, os problemas de Valoração e Interpolação, com base na Matriz de Fourier.
Valoração Y = ν k ( w ) X = ν k ( w ) P k P k − 1 X = ( ν k ( w ) P k ) ( P k X ) = F k ( w ) ( P k X ) \begin{aligned} Y &= \nu_k(w)X \\ &= \nu_k(w)P_kP_k^{-1}X \\ &= (\nu_k(w)P_k)(P_kX) \\ &= F_k(w)(P_kX) \end{aligned} Y = ν k ( w ) X = ν k ( w ) P k P k − 1 X = ( ν k ( w ) P k ) ( P k X ) = F k ( w ) ( P k X ) Interpolação X = 1 r ν k ( w ) † Y = 1 r ν k ( w ) † P k P k Y = 1 r ν k ( w ) † P k † P k † Y = 1 r ( ν k ( w ) P k ) † ( P k Y † ) † = 1 r F k ( w ) † ( P k Y † ) † = 1 r F k ( w ) † ( P k Y † ) † = 1 r [ F k ( w ) ( P k Y † ) ] † = 1 r F k ( w ) ( P k Y † ) \begin{aligned}
X &=\frac 1 r \nu_k(w)^\dagger Y \\
&= \frac 1 r \nu_k(w)^\dagger P_kP_kY \\
&= \frac 1 r \nu_k(w)^\dagger P_k^\dagger P_k^\dagger Y \\
&= \frac 1 r (\nu_k(w) P_k)^\dagger (P_kY^\dagger)^\dagger\\
&= \frac 1 r F_k(w)^\dagger (P_kY^\dagger)^\dagger \\
&= \frac 1 r F_k(w)^\dagger (P_kY^\dagger)^\dagger\\
&= \frac 1 r [F_k(w) (P_kY^\dagger)]^\dagger\\
&= \frac 1 r F_k(w) (P_kY^\dagger)
\end{aligned} X = r 1 ν k ( w ) † Y = r 1 ν k ( w ) † P k P k Y = r 1 ν k ( w ) † P k † P k † Y = r 1 ( ν k ( w ) P k ) † ( P k Y † ) † = r 1 F k ( w ) † ( P k Y † ) † = r 1 F k ( w ) † ( P k Y † ) † = r 1 [ F k ( w ) ( P k Y † ) ] † = r 1 F k ( w ) ( P k Y † ) Para todo o k ∈ N 0 k \in \N_0 k ∈ N 0 Matriz de Fourier F k ( w ) F_k(w) F k ( w )
F 0 ( 1 ) = 1 F k + 1 = [ F k ( w 2 ) D k F k ( w 2 ) F k ( w 2 ) − D k F k ( w 2 ) ] F_0(1) = 1 \\
F_{k+1} = \begin{bmatrix}F_k(w^2) & D_kF_k(w^2)\\ F_k(w^2) & -D_kF_k(w^2)\end{bmatrix} F 0 ( 1 ) = 1 F k + 1 = [ F k ( w 2 ) F k ( w 2 ) D k F k ( w 2 ) − D k F k ( w 2 ) ] Esta estrutura recursiva é a base do algoritmo FFT .
Exemplo p 1 ( n ) = n + 1 p 2 ( n ) = 3 n + 2 q ( n ) = p 1 ( n ) × p 2 ( n ) p_1(n) = n + 1 \\ p_2(n) = 3n+2 \\
q(n) = p_1(n) \times p_2(n) p 1 ( n ) = n + 1 p 2 ( n ) = 3 n + 2 q ( n ) = p 1 ( n ) × p 2 ( n ) Queremos determinar q ( n ) q(n) q ( n )
Passo 1 1 1 1 2 2 2 ( 1 + 1 ) (1+1) ( 1 + 1 ) 3 3 3 ( grau + 1 ) (\text{grau}+1) ( grau + 1 ) k ∈ N k \in \N k ∈ N 2 k ≥ 3 2^k \geq 3 2 k ≥ 3 2 2 2 2 2 2^2 2 2 ( 1 , 1 , 0 , 0 ) (1,1,0,0) ( 1 , 1 , 0 , 0 ) ( 2 , 3 , 0 , 0 ) (2,3,0,0) ( 2 , 3 , 0 , 0 ) Passo 2 Rev k \operatorname{Rev}_k Rev k k = 2 k=2 k = 2
00 01 10 11 00 01 10 11 ( 1 , 1 , 0 , 0 ) ( 2 , 3 , 0 , 0 ) ( 1 , 0 , 1 , 0 ) ( 2 , 0 , 3 , 0 ) \begin{matrix}
00 & 01 & 10 & 11 && 00 & 01 & 10 & 11 \\
(1, & 1, & 0, & 0) && (2, & 3, & 0, & 0) \\
(1, & 0, & 1, & 0) && (2, & 0, & 3, & 0)
\end{matrix} 00 ( 1 , ( 1 , 01 1 , 0 , 10 0 , 1 , 11 0 ) 0 ) 00 ( 2 , ( 2 , 01 3 , 0 , 10 0 , 3 , 11 0 ) 0 ) Passo 3
F 2 ( i ) [ 1 0 1 0 ] = [ F 1 ( − 1 ) D 1 F 1 ( − 1 ) F 1 ( − 1 ) − D 1 F 1 ( − 1 ) ] [ 1 0 1 0 ] = [ [ 1 1 1 − 1 ] [ 1 0 ] + [ 1 0 0 i ] [ 1 1 1 − 1 ] [ 1 0 ] [ 1 1 1 − 1 ] [ 1 0 ] − [ 1 0 0 i ] [ 1 1 1 − 1 ] [ 1 0 ] ] = [ [ 1 1 ] + [ 1 0 0 i ] [ 1 1 ] [ 1 1 ] − [ 1 0 0 i ] [ 1 1 ] ] = [ 2 1 + i 0 1 − i ] F_2(i) \begin{bmatrix}1\\0\\1\\0\end{bmatrix}= \begin{bmatrix}F_1(-1) & D_1F_1(-1)\\ F_1(-1) & -D_1F_1(-1)\end{bmatrix}\begin{bmatrix}1\\0\\1\\0\end{bmatrix}\\
= \begin{bmatrix}
\begin{bmatrix}1&1\\1&-1\end{bmatrix}
\begin{bmatrix}1\\0\end{bmatrix}+
\begin{bmatrix}1 & 0 \\ 0 & i\end{bmatrix}
\begin{bmatrix}1&1\\1&-1\end{bmatrix}
\begin{bmatrix}1\\0\end{bmatrix}\\
\begin{bmatrix}1&1\\1&-1\end{bmatrix}
\begin{bmatrix}1\\0\end{bmatrix}-
\begin{bmatrix}1 & 0 \\ 0 & i\end{bmatrix}
\begin{bmatrix}1&1\\1&-1\end{bmatrix}\begin{bmatrix}1\\0\end{bmatrix}
\end{bmatrix}\\
=\begin{bmatrix}
\begin{bmatrix}1\\1\end{bmatrix}+\begin{bmatrix}1 & 0 \\ 0 & i\end{bmatrix}\begin{bmatrix}1\\1\end{bmatrix}\\
\begin{bmatrix}1\\1\end{bmatrix}-\begin{bmatrix}1 & 0 \\ 0 & i\end{bmatrix}\begin{bmatrix}1\\1\end{bmatrix}
\end{bmatrix}\\
=\begin{bmatrix}2\\1+i\\0\\1-i\end{bmatrix} F 2 ( i ) 1 0 1 0 = [ F 1 ( − 1 ) F 1 ( − 1 ) D 1 F 1 ( − 1 ) − D 1 F 1 ( − 1 ) ] 1 0 1 0 = [ 1 1 1 − 1 ] [ 1 0 ] + [ 1 0 0 i ] [ 1 1 1 − 1 ] [ 1 0 ] [ 1 1 1 − 1 ] [ 1 0 ] − [ 1 0 0 i ] [ 1 1 1 − 1 ] [ 1 0 ] = [ 1 1 ] + [ 1 0 0 i ] [ 1 1 ] [ 1 1 ] − [ 1 0 0 i ] [ 1 1 ] = 2 1 + i 0 1 − i Relembrar que ( 2 , 1 + i , 0 , 1 − i ) (2,1+i,0,1-i) ( 2 , 1 + i , 0 , 1 − i ) p 1 ( n ) p_1(n) p 1 ( n ) n n n 2 2 2^2 2 2 ( 1 , i , − 1 , − i ) (1,i,-1,-i) ( 1 , i , − 1 , − i )
F 2 ( i ) [ 2 0 3 0 ] = [ F 1 ( − 1 ) D 1 F 1 ( − 1 ) F 1 ( − 1 ) − D 1 F 1 ( − 1 ) ] [ 2 0 3 0 ] = [ [ 1 1 1 − 1 ] [ 2 0 ] + [ 1 0 0 i ] [ 1 1 1 − 1 ] [ 3 0 ] [ 1 1 1 − 1 ] [ 2 0 ] − [ 1 0 0 i ] [ 1 1 1 − 1 ] [ 3 0 ] ] = [ [ 2 2 ] + [ 1 0 0 i ] [ 3 3 ] [ 2 2 ] − [ 1 0 0 i ] [ 3 3 ] ] = [ 5 2 + 3 i − 1 2 − 3 i ] F_2(i) \begin{bmatrix}2\\0\\3\\0\end{bmatrix}= \begin{bmatrix}F_1(-1) & D_1F_1(-1)\\ F_1(-1) & -D_1F_1(-1)\end{bmatrix}\begin{bmatrix}2\\0\\3\\0\end{bmatrix}\\
= \begin{bmatrix}
\begin{bmatrix}1&1\\1&-1\end{bmatrix}
\begin{bmatrix}2\\0\end{bmatrix}+
\begin{bmatrix}1 & 0 \\ 0 & i\end{bmatrix}
\begin{bmatrix}1&1\\1&-1\end{bmatrix}
\begin{bmatrix}3\\0\end{bmatrix}\\
\begin{bmatrix}1&1\\1&-1\end{bmatrix}
\begin{bmatrix}2\\0\end{bmatrix}-
\begin{bmatrix}1 & 0 \\ 0 & i\end{bmatrix}
\begin{bmatrix}1&1\\1&-1\end{bmatrix}\begin{bmatrix}3\\0\end{bmatrix}
\end{bmatrix}\\
=\begin{bmatrix}
\begin{bmatrix}2\\2\end{bmatrix}+\begin{bmatrix}1 & 0 \\ 0 & i\end{bmatrix}\begin{bmatrix}3\\3\end{bmatrix}\\~\\
\begin{bmatrix}2\\2\end{bmatrix}-\begin{bmatrix}1 & 0 \\ 0 & i\end{bmatrix}\begin{bmatrix}3\\3\end{bmatrix}
\end{bmatrix}\\
=\begin{bmatrix}5\\2+3i\\-1\\2-3i\end{bmatrix} F 2 ( i ) 2 0 3 0 = [ F 1 ( − 1 ) F 1 ( − 1 ) D 1 F 1 ( − 1 ) − D 1 F 1 ( − 1 ) ] 2 0 3 0 = [ 1 1 1 − 1 ] [ 2 0 ] + [ 1 0 0 i ] [ 1 1 1 − 1 ] [ 3 0 ] [ 1 1 1 − 1 ] [ 2 0 ] − [ 1 0 0 i ] [ 1 1 1 − 1 ] [ 3 0 ] = [ 2 2 ] + [ 1 0 0 i ] [ 3 3 ] [ 2 2 ] − [ 1 0 0 i ] [ 3 3 ] = 5 2 + 3 i − 1 2 − 3 i Passo 4
( 2 , 1 + i , 0 , 1 − i ) ⊗ ( 5 , 2 + 3 i , − 1 , 2 − 3 i ) = = ( 10 , − 1 + 5 i , 0 , − 1 − 5 i ) (2,1+i,0,1-i) \otimes (5,2+3i,-1,2-3i) = \\
=(10, -1+5i,0, -1-5i) ( 2 , 1 + i , 0 , 1 − i ) ⊗ ( 5 , 2 + 3 i , − 1 , 2 − 3 i ) = = ( 10 , − 1 + 5 i , 0 , − 1 − 5 i ) Estes são os valores do polinómio produto, ainda desconhecido, nos pontos 1 , i , − 1 , − i 1,i,-1,-i 1 , i , − 1 , − i Passo 5 Rev 2 \operatorname{Rev}_2 Rev 2
( 10 , − 1 + 5 i , 0 , − 1 − 5 i ) → ( 10 , − 1 − 5 i , 0 , − 1 + 5 i ) ( 10 , − 1 − 5 i , 0 , − 1 + 5 i ) ( 10 , 0 , − 1 − 5 i , − 1 + 5 i ) (10,-1+5i,0,-1-5i) \rightarrow (10,-1-5i,0,-1+5i) \\
\\
\begin{matrix}
(10, & -1-5i, & 0, & -1+5i) \\
(10, & 0, & -1-5i, & -1+5i)
\end{matrix} ( 10 , − 1 + 5 i , 0 , − 1 − 5 i ) → ( 10 , − 1 − 5 i , 0 , − 1 + 5 i ) ( 10 , ( 10 , − 1 − 5 i , 0 , 0 , − 1 − 5 i , − 1 + 5 i ) − 1 + 5 i ) Passo 6
F 2 ( i ) [ 10 0 − 1 − 5 i − 1 + 5 i ] = [ F 1 ( − 1 ) D 1 F 1 ( − 1 ) F 1 ( − 1 ) − D 1 F 1 ( − 1 ) ] [ 10 0 − 1 − 5 i − 1 + 5 i ] = [ [ 1 1 1 − 1 ] [ 10 0 ] + [ 1 0 0 i ] [ 1 1 1 − 1 ] [ − 1 − 5 i − 1 + 5 i ] [ 1 1 1 − 1 ] [ 10 0 ] − [ 1 0 0 i ] [ 1 1 1 − 1 ] [ − 1 − 5 i − 1 + 5 i ] ] = [ [ 10 10 ] + [ 1 0 0 i ] [ − 2 − 10 i ] [ 10 10 ] − [ 1 0 0 i ] [ − 2 − 10 i ] ] = [ 8 20 12 0 ] F_2(i) \begin{bmatrix}10\\0\\-1-5i\\-1+5i\end{bmatrix}= \begin{bmatrix}F_1(-1) & D_1F_1(-1)\\ F_1(-1) & -D_1F_1(-1)\end{bmatrix}\begin{bmatrix}10\\0\\-1-5i\\-1+5i\end{bmatrix}\\
= \begin{bmatrix}
\begin{bmatrix}1&1\\1&-1\end{bmatrix}
\begin{bmatrix}10\\0\end{bmatrix}+
\begin{bmatrix}1 & 0 \\ 0 & i\end{bmatrix}
\begin{bmatrix}1&1\\1&-1\end{bmatrix}
\begin{bmatrix}-1-5i\\-1+5i\end{bmatrix}\\
\begin{bmatrix}1&1\\1&-1\end{bmatrix}
\begin{bmatrix}10\\0\end{bmatrix}-
\begin{bmatrix}1 & 0 \\ 0 & i\end{bmatrix}
\begin{bmatrix}1&1\\1&-1\end{bmatrix}\begin{bmatrix}-1-5i\\-1+5i\end{bmatrix}
\end{bmatrix}\\
=\begin{bmatrix}
\begin{bmatrix}10\\10\end{bmatrix}+\begin{bmatrix}1 & 0 \\ 0 & i\end{bmatrix}\begin{bmatrix}-2\\-10i\end{bmatrix}\\
\begin{bmatrix}10\\10\end{bmatrix}-\begin{bmatrix}1 & 0 \\ 0 & i\end{bmatrix}\begin{bmatrix}-2\\-10i\end{bmatrix}
\end{bmatrix}\\
=\begin{bmatrix}8\\20\\12\\0\end{bmatrix} F 2 ( i ) 10 0 − 1 − 5 i − 1 + 5 i = [ F 1 ( − 1 ) F 1 ( − 1 ) D 1 F 1 ( − 1 ) − D 1 F 1 ( − 1 ) ] 10 0 − 1 − 5 i − 1 + 5 i = [ 1 1 1 − 1 ] [ 10 0 ] + [ 1 0 0 i ] [ 1 1 1 − 1 ] [ − 1 − 5 i − 1 + 5 i ] [ 1 1 1 − 1 ] [ 10 0 ] − [ 1 0 0 i ] [ 1 1 1 − 1 ] [ − 1 − 5 i − 1 + 5 i ] = [ 10 10 ] + [ 1 0 0 i ] [ − 2 − 10 i ] [ 10 10 ] − [ 1 0 0 i ] [ − 2 − 10 i ] = 8 20 12 0 Passo 7 2 2 = 4 2^2=4 2 2 = 4
( 8 , 20 , 12 , 0 ) → ( 2 , 5 , 3 , 0 ) (8,20,12,0) \rightarrow (2,5,3,0) ( 8 , 20 , 12 , 0 ) → ( 2 , 5 , 3 , 0 ) Podemos concluir:
q ( n ) = 2 + 5 n + 3 n 2 q(n) = 2 + 5n + 3n^2 q ( n ) = 2 + 5 n + 3 n 2 ATENÇÃO: Como os polinómios iniciais tinham valores inteiros e reais, o polinómio produto também terá. Se o resultado não for inteiro ou real, nestes casos, houve um erro de contas.
Para exemplos com k = 3 k = 3 k = 3