Se tivermos acesso às respetivas tabelas dos números de Stirling, é possível encurtar bastante um problema como descobrir a soma fechada para ∑ k = 0 n − 1 k 3 \sum_{k=0}^{n-1}k^3 ∑ k = 0 n − 1 k 3
∑ k = 0 n − 1 k 3 = ∑ k = 0 n − 1 ( { 3 0 } k 0 ‾ + { 3 1 } k 1 ‾ + { 3 2 } k 2 ‾ + { 3 3 } k 3 ‾ ) = ∑ k = 0 n − 1 ( 0 k 0 ‾ + 1 k 1 ‾ + 3 k 2 ‾ + 1 k 3 ‾ ) \sum_{k=0}^{n-1}k^3 =\\ \sum_{k=0}^{n-1}\left(\begin{Bmatrix}3\\0\end{Bmatrix}k^{\underline0} + \begin{Bmatrix}3\\1\end{Bmatrix}k^{\underline1} +
\begin{Bmatrix}3\\2\end{Bmatrix}k^{\underline2} +
\begin{Bmatrix}3\\3\end{Bmatrix}k^{\underline3}\right) =\\\sum_{k=0}^{n-1}\left(0k^{\underline0} + 1k^{\underline1} + 3k^{\underline2} + 1k^{\underline3}\right) k = 0 ∑ n − 1 k 3 = k = 0 ∑ n − 1 ( { 3 0 } k 0 + { 3 1 } k 1 + { 3 2 } k 2 + { 3 3 } k 3 ) = k = 0 ∑ n − 1 ( 0 k 0 + 1 k 1 + 3 k 2 + 1 k 3 ) Que dá:
[ 1 2 k 2 ‾ + k 3 ‾ + 1 4 k 4 ‾ ] 0 n \left[\frac{1}{2}k^{\underline2} + k^{\underline3}+\frac{1}{4}k^{\underline4}\right]_0^{n} [ 2 1 k 2 + k 3 + 4 1 k 4 ] 0 n Agora, recorrendo à tabela:
k 0 k 1 k 2 k 3 k 4 k 2 ‾ 2 0 − 1 2 1 2 0 0 k 3 ‾ 0 2 − 3 1 0 k 4 ‾ 4 0 − 3 2 11 4 − 3 2 1 4 \begin{array}{ c | c c c c c c c }
& \\
& k^{0} & k^{1} & k^{2} & k^{3} & k^{4}\\
\hline &\\
\frac{k^{\underline{2}}}{2} & 0 & -\frac{1}{2} & \frac{1}{2} & 0 & 0 \\
&\\
k^{\underline{3}} & 0 & 2 & -3 & 1 & 0 \\
&\\
\frac{k^{\underline{4}}}{4} & 0 & -\frac{3}{2} & \frac{11}{4} & -\frac{3}{2} & \frac{1}{4} \\
\end{array} 2 k 2 k 3 4 k 4 k 0 0 0 0 k 1 − 2 1 2 − 2 3 k 2 2 1 − 3 4 11 k 3 0 1 − 2 3 k 4 0 0 4 1 tem-se, então:
∑ k = 0 n − 1 k 3 = [ 1 4 k 2 − 1 2 k 3 + 1 4 k 4 ] 0 n = 1 4 n 2 − 1 2 n 3 + 1 4 n 4 = ( n ( n − 1 ) 2 ) 2 = ( ∑ k = 0 n − 1 k ) 2 \sum_{k=0}^{n-1}k^3 = \left[\frac{1}{4}k^2 - \frac{1}{2}k^3+\frac{1}{4}k^4\right]_0^n =\frac{1}{4}n^2 - \frac{1}{2}n^3+\frac{1}{4}n^4 =\\ \left(\frac{n(n-1)}{2}\right)^2 = \left(\sum_{k=0}^{n-1}k\right)^2 k = 0 ∑ n − 1 k 3 = [ 4 1 k 2 − 2 1 k 3 + 4 1 k 4 ] 0 n = 4 1 n 2 − 2 1 n 3 + 4 1 n 4 = ( 2 n ( n − 1 ) ) 2 = ( k = 0 ∑ n − 1 k ) 2 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 \begin{array}{ c c c c c c c }
1 & & & & & & \\
1 & 1 & & & & & \\
1 & 2 & 1 & & & & \\
1 & \smartcolor{orange} 3 & \smartcolor{orange}3 & 1 & & & \\
1 & 4 & \smartcolor{orange}6 & 4 & 1 & & \\
1 & 5 & 10 & 10 & 5 & 1 & \\
1 & 6 & 15 & 20 & 15 & 6 & 1
\end{array}\\ 1 1 1 1 1 1 1 1 2 3 4 5 6 1 3 6 10 15 1 4 10 20 1 5 15 1 6 1 ∀ n ∈ N ( n 0 ) = 1 \forall_{n \in \mathbb N} {n \choose 0} = 1 ∀ n ∈ N ( 0 n ) = 1 ∀ n ∈ N ( ( i > n ) ⟹ ( n i ) = 0 ) ) \forall_{n \in \mathbb N} \left( (i > n) \implies {n \choose i} = 0) \right) ∀ n ∈ N ( ( i > n ) ⟹ ( i n ) = 0 ) ) ∀ n ∈ N ∀ i ∈ N ( ( 0 < i ≤ n ) ⟹ ( n i ) = ( n − 1 i − 1 ) + ( n − 1 i ) ) \forall_{n \in \mathbb N} \forall_{i \in \mathbb N} \left( ( 0 < i \leq n) \implies {n \choose i} = {n-1 \choose i-1} + {n-1 \choose i}\right) ∀ n ∈ N ∀ i ∈ N ( ( 0 < i ≤ n ) ⟹ ( i n ) = ( i − 1 n − 1 ) + ( i n − 1 ) ) e, claro:
( n i ) = n ! ( n − i ) ! i ! {n \choose i} = \frac{n!}{(n-i)!\ i!} ( i n ) = ( n − i )! i ! n ! 0 1 2 3 4 5 k 0 k 1 k 2 k 3 k 4 k 5 0 k 0 ‾ 1 0 0 0 0 0 1 k 1 ‾ 0 1 0 0 0 0 2 k 2 ‾ 0 − 1 1 0 0 0 3 k 3 ‾ 0 2 − 3 1 0 0 4 k 4 ‾ 0 − 6 11 − 6 1 0 5 k 5 ‾ 0 24 − 50 35 − 10 1 \begin{array}{ c c c c c c c c }
& & 0 & 1 & 2 & 3 & 4 & 5\\
& & k^{0} & k^{1} & k^{2} & k^{3} & k^{4} & k^{5}\\
0 & k^{\underline{0}} & 1 & 0 & 0 & 0 & 0 & 0\\
1 & k^{\underline{1}} & 0 & 1 & 0 & 0 & 0 & 0\\
2 & k^{\underline{2}} & 0 & -1 & 1 & 0 & 0 & 0\\
3 & k^{\underline{3}} & 0 & 2 & -3 & 1 & 0 & 0\\
\smartcolor{orange} 4 & k^{\underline{4}} & 0 & -6 & \smartcolor{orange} {11} & \smartcolor{orange} {-6} & 1 & 0\\
5 & k^{\underline{5}} & 0 & 24 & -50 & \smartcolor{orange} {35} & -10 & 1
\end{array} 0 1 2 3 4 5 k 0 k 1 k 2 k 3 k 4 k 5 0 k 0 1 0 0 0 0 0 1 k 1 0 1 − 1 2 − 6 24 2 k 2 0 0 1 − 3 11 − 50 3 k 3 0 0 0 1 − 6 35 4 k 4 0 0 0 0 1 − 10 5 k 5 0 0 0 0 0 1 Propriedades
∀ n ∈ N [ n 0 ] = ( n = = 0 ) \forall_{n \in \mathbb N} \begin{bmatrix} n \\ 0\end{bmatrix} = (n == 0) ∀ n ∈ N [ n 0 ] = ( n == 0 ) ∀ n ∈ N ( ( i > n ) ⟹ [ n i ] = 0 ) \forall_{n \in \mathbb N} \left( (i > n) \implies \begin{bmatrix} n \\ i\end{bmatrix} = 0 \right) ∀ n ∈ N ( ( i > n ) ⟹ [ n i ] = 0 ) ∀ n ∈ N ∀ i ∈ N ( ( 0 < i ≤ n ) ⟹ [ n i ] = [ n − 1 i − 1 ] − ( n − 1 ) [ n − 1 i ] ) \forall_{n \in \mathbb N} \forall_{i \in \mathbb N} \left( ( 0 < i \leq n) \implies \begin{bmatrix} n \\ i\end{bmatrix} = \begin{bmatrix} n-1 \\ i-1\end{bmatrix} - (n-1)\begin{bmatrix} n-1 \\ i\end{bmatrix}\right) ∀ n ∈ N ∀ i ∈ N ( ( 0 < i ≤ n ) ⟹ [ n i ] = [ n − 1 i − 1 ] − ( n − 1 ) [ n − 1 i ] ) 0 1 2 3 4 5 6 k 0 ‾ k 1 ‾ k 2 ‾ k 3 ‾ k 4 ‾ k 5 ‾ k 6 ‾ 0 k 0 1 0 0 0 0 0 0 1 k 1 0 1 0 0 0 0 0 2 k 2 0 1 1 0 0 0 0 3 k 3 0 1 3 1 0 0 0 4 k 4 0 1 7 6 1 0 0 5 k 5 0 1 15 25 10 1 0 6 k 6 0 1 31 90 65 15 1 \begin{array}{ c c c c c c c c }
& & 0 & 1 & 2 & \smartcolor{orange} 3 & 4 & 5 & 6\\
& & k^{\underline{0}} & k^{\underline{1}} & k^{\underline{2}} & k^{\underline{3}} & k^{\underline{4}} & k^{\underline{5}} & k^{\underline{6}}\\
0 & k^{0} & 1 & 0 & 0 & 0 & 0 & 0 & 0\\
1 & k^{1} & 0 & 1 & 0 & 0 & 0 & 0 & 0\\
2 & k^{2} & 0 & 1 & 1 & 0 & 0 & 0 & 0\\
3 & k^{3} & 0 & 1 & 3 & 1 & 0 & 0 & 0\\
4 & k^{4} & 0 & 1 & 7 & 6 & 1 & 0 & 0\\
5 & k^{5} & 0 & 1 & \smartcolor{orange} {15} & \smartcolor{orange}{25} & 10 & 1 & 0\\
6 & k^{6} & 0 & 1 & 31 & \smartcolor{orange}{90} & 65 & 15 & 1
\end{array} 0 1 2 3 4 5 6 k 0 k 1 k 2 k 3 k 4 k 5 k 6 0 k 0 1 0 0 0 0 0 0 1 k 1 0 1 1 1 1 1 1 2 k 2 0 0 1 3 7 15 31 3 k 3 0 0 0 1 6 25 90 4 k 4 0 0 0 0 1 10 65 5 k 5 0 0 0 0 0 1 15 6 k 6 0 0 0 0 0 0 1 Propriedades
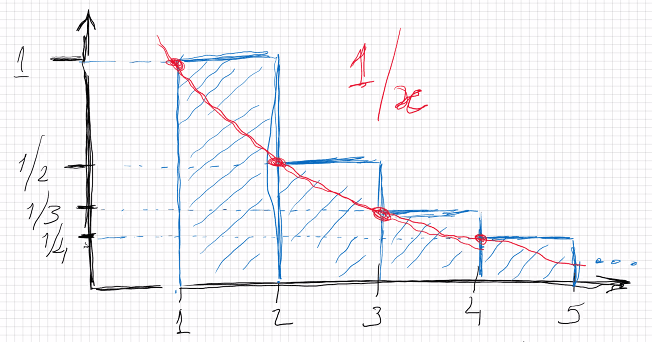
∀ n ∈ N { n 0 } = ( n = = 0 ) \forall_{n \in \mathbb N} \begin{Bmatrix} n \\ 0\end{Bmatrix} = (n == 0) ∀ n ∈ N { n 0 } = ( n == 0 ) ∀ n ∈ N ( ( i > n ) ⟹ { n i } = 0 ) ) \forall_{n \in \mathbb N} \left( (i > n) \implies \begin{Bmatrix} n \\ i\end{Bmatrix} = 0) \right) ∀ n ∈ N ( ( i > n ) ⟹ { n i } = 0 ) ) ∀ n ∈ N ∀ i ∈ N ( ( 0 < i ≤ n ) ⟹ { n i } = { n − 1 i − 1 } + i { n − 1 i } ) \forall_{n \in \mathbb N} \forall_{i \in \mathbb N} \left( ( 0 < i \leq n) \implies \begin{Bmatrix} n \\ i\end{Bmatrix} = \begin{Bmatrix} n-1 \\ i-1\end{Bmatrix} +i\begin{Bmatrix} n-1 \\ i\end{Bmatrix}\right) ∀ n ∈ N ∀ i ∈ N ( ( 0 < i ≤ n ) ⟹ { n i } = { n − 1 i − 1 } + i { n − 1 i } ) Gráfico de 1 x \frac{1}{x} x 1
Sendo H n = ∑ k = 1 n 1 k H_n = \sum_{k=1}^{n}\frac{1}{k} H n = ∑ k = 1 n k 1
H n − 1 < l n ( n ) < H n H_n - 1 <ln(n) <H_n H n − 1 < l n ( n ) < H n e
H n = { 0 s e n = 0 ∑ k = 1 n 1 k s e n > 0 H_n = \begin{cases}\ 0\quad se\quad n=0 \\ \sum_{k=1}^n\frac{1}{k}\quad se\quad n>0\end{cases} H n = { 0 se n = 0 ∑ k = 1 n k 1 se n > 0 cuja derivada ou diferença finita é:
Δ H n = H n + 1 − H n = H n + 1 n + 1 − H n = 1 n + 1 = n − 1 ‾ \Delta H_n = H_{n+1}-H_n = H_n+\frac 1 {n+1} - H_n = \frac 1 {n+1} = n^{\underline{-1}} Δ H n = H n + 1 − H n = H n + n + 1 1 − H n = n + 1 1 = n − 1 Assim, é possível agora calcular o seguinte tipo de somas fechadas:
∑ k = 0 n − 1 k − 1 ‾ = ∑ k = 0 n − 1 Δ H k = [ H k ] 0 n = H n \sum_{k=0}^{n-1}k^{\underline{-1}} = \sum_{k=0}^{n-1}\Delta H_k = \left[H_k\right]_0^n = H_n k = 0 ∑ n − 1 k − 1 = k = 0 ∑ n − 1 Δ H k = [ H k ] 0 n = H n Outros resultados:
∑ k = 0 n − 1 H k = Δ ( k H k ) = ( k + 1 ) H k + 1 − k H k = ( k + 1 ) ( H k + 1 k + 1 ) − k H k = ( k + 1 ) H k + 1 − k H k = H k + 1 ⇔ H k = Δ ( k H k ) − 1 \sum_{k=0}^{n-1}H_k= \\
\Delta (kH_k) =(k+1)H_{k+1} -kH_k = \\ (k+1)(H_k + \frac 1 {k+1}) -kH_k = \\
(k+1)H_k +1 -kH_k = \\
H_k +1 \\
\Leftrightarrow
H_k = \Delta (kH_k)-1 k = 0 ∑ n − 1 H k = Δ ( k H k ) = ( k + 1 ) H k + 1 − k H k = ( k + 1 ) ( H k + k + 1 1 ) − k H k = ( k + 1 ) H k + 1 − k H k = H k + 1 ⇔ H k = Δ ( k H k ) − 1 ou seja:
∑ k = 0 n − 1 H k = n H n − n \sum_{k=0}^{n-1}H_k = nH_n - n k = 0 ∑ n − 1 H k = n H n − n Se quiséssemos calcular ∑ k = 0 n − 1 k H k \displaystyle \sum_{k=0}^{n-1}kH_k k = 0 ∑ n − 1 k H k k 2 ‾ 2 H k \frac{k^{\underline2}}{2} H_k 2 k 2 H k
Δ ( k 2 ‾ 2 H k ) = 1 2 k ( k + 1 ) H k + 1 − 1 2 k ( k − 1 ) H k = 1 2 k ( k + 1 ) ( H k + 1 k + 1 ) − 1 2 k ( k − 1 ) H k = 1 2 k H k ( k + 1 − ( k − 1 ) ) + 1 2 k = k H k + 1 2 k ⇔ k H k = Δ ( k 2 ‾ 2 H k ) − 1 2 k \Delta \left(\frac{k^{\underline{2}}}{2}H_k\right) = \frac 1 2 k(k+1)H_{k+1} - \frac 1 2k(k-1)H_k \\
= \frac 1 2k(k+1)\left(H_k + \frac 1 {k+1}\right) - \frac 1 2k(k-1)H_k \\
=\frac 1 2kH_k(k+1-(k-1)) + \frac 1 2k \\
= kH_k + \frac 1 2 k \\
\Leftrightarrow kH_k = \Delta\left(\frac{k^{\underline2}}{2}H_k\right)-\frac 1 2k Δ ( 2 k 2 H k ) = 2 1 k ( k + 1 ) H k + 1 − 2 1 k ( k − 1 ) H k = 2 1 k ( k + 1 ) ( H k + k + 1 1 ) − 2 1 k ( k − 1 ) H k = 2 1 k H k ( k + 1 − ( k − 1 )) + 2 1 k = k H k + 2 1 k ⇔ k H k = Δ ( 2 k 2 H k ) − 2 1 k Chegou-se assim, a uma fórmula parecida à da primitivação por partes.