Grafos - Início

O que é um Grafo?

Um grafo é um par $g = (V,R)$ , onde:

$V$ é um conjunto de vértices finito e não vazio
$R$ é o conjunto dos dos pares de vértices que estão ligados por uma aresta

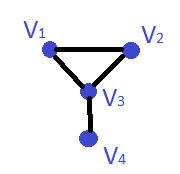
Por exemplo

V = \{V_1,V_2,V_3,V_4\}\\ R = \{(V_1,V_2),(V_2,V_1),(V_2,V_3),(V_3,V_2),(V_1,V_3),(V_3,V_1),(V_3,V_4),(V_4,V_3),\}

Como uma aresta não tem direção, em $R$ representa-se os dois pares das $2$ "direções" de cada aresta.
Contudo, como isto é uma propriedade conhecida dos grafos, também se pode represente um grafo $g$ por $g = (R,E)$ , onde $E$ é o conjunto $R$ sem repetições.

No caso do exemplo acima, um $E$ possível seria

E = \{(V_1,V_2),(V_3,V_2),(V_4,V_3),(V_1,V_3)\}

Definições e Teoremas

Ordem e Tamanho do grafo

Ordem do grafo, $p$ , é o número de vértices do grafo.
Tamanho do grafo, $q$ , é o número de arestas do grafo

Seja $g = (V,E)$ ,

p = \#V\\ q = \#E

Relembrar

$\#A$ = número de elementos do conjunto $A$

Grau de um vértice

$g = (V,E)$ . Para um vértice $v\in V$ , o seu grau em $g$ corresponde ao número de arestas de $g$ que incidem em $v$ .
Representa-se por:

\operatorname{deg}_g(v)

Teorema Fundamental da Teoria dos Grafos

Num grafo $g=(V,E)$ , a soma dos graus dos seus vértices é igual ao dobro do Tamanho do grafo.

Demonstração

Primeiro define-se a seguinte operação

\operatorname{I}:V \times E \rightarrow \{0,1\}

Seja $v$ um vértice e $e$ uma aresta de $g$ ,
$\operatorname{I}(v,e) =$ número de vezes que a aresta $e$ incide em $v$

Seja $S_{deg}$ a soma dos graus dos vértices de $g$ ,

S_{deg} = \sum_{v \in V} \operatorname{deg}_g(v)\\ =\sum_{v \in V} \sum_{e \in E} \operatorname{I}(i,e)\\ = \sum_{e \in E} \sum_{v \in V} \operatorname{I}(i,e)\\ = \sum_{e \in E} 2 = 2 \times (\#E)

QED

$\sum_{v \in V} \operatorname{I}(i,e)$ é 2, pois cada aresta $e$ está associada a 2 vértices.

Teorema 2

Num grafo $g = (V,E)$ , o número dos seus vértices ímpares é par.

NOTA

vértice é par/ímpar $\rightarrow$ tem grau par/ímpar.

Demonstração

Para $g = (V,E)$ , onde $\#V=p$

V = \{v_1,\dots,v_k,u_1,\dots,u_{p-k}\}\\ v_1,\dots,v_k \rightarrow \text{vértices pares}\\ u_1,\dots,u_{p-k} \rightarrow \text{vértices ímpares}

Pelo Teorema Fundamental da Teoria dos Grafos, a soma dos graus é $2\times q$ , com $q$ o número de arestas.
Assim sendo, será um número par. Como a soma dos graus dos vértices pares é par, para o resultado final também ser par, é obrigatório haver um número par de vértices ímpares.

QED

Aplicações

Exercício 5 da Série 4
Um certa comissão parlamentar da Assembleia da República é composta por 15 deputados. Conclua que não é possível que cada um deles já tenha estado em comissões parlamentares anteriores com exatamente 5 dos outros deputados que fazem parte desta comissão.

Se se desenhar um grafo onde os vértices são os deputados e as arestas ligam dois deputados que tenham estado juntos em comissões anteriores, o grafo teria um número ímpar $(15)$ de vértices com grau ímpar $(5)$ , o que pelo Teorema 2 é impossível.

QED

Grafo Regular

Um grafo diz-se regular se todos os seus vértices têm o mesmo grau.
Um grafo diz-se $k$ -regular $(k \in N)$ se os seus vértices têm grau $k$ .

Exemplo

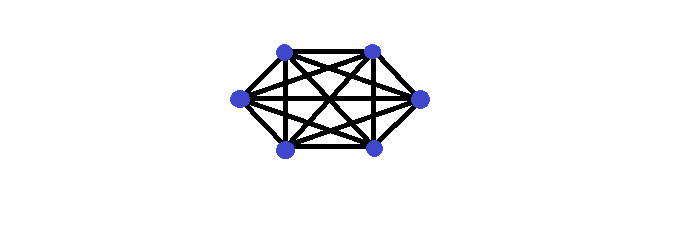
Grafo Completo

Um grafo diz-se completo quando cada par de vértices constitui uma aresta (está tudo ligado).

Exemplo

NOTA

Todo o grafo completo de $k$ vértices é $k$ -1 regular
$\binom{p}{2} = \frac{p(p-1)}{2}$ é o número máximo de arestas que um grafo pode ter
$K_n \rightarrow$ grafo completo de $n$ vértices

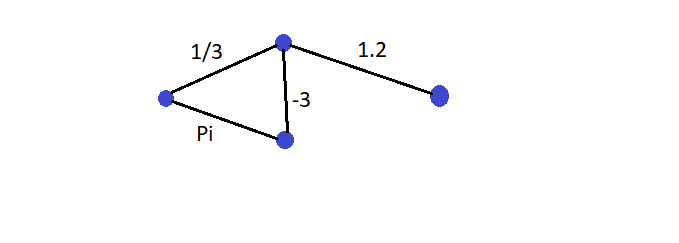
Rede

É um terno $N = (V,E,\operatorname{f})$ , onde $g=(V,E)$ é um grafo subjacente à Rede e $\operatorname{f}: E \rightarrow \R$ uma aplicação (todos os elementos de $E$ têm correspondência).

Em suma, uma Rede é um grafo onde as arestas têm valores reais associados.

Exemplo

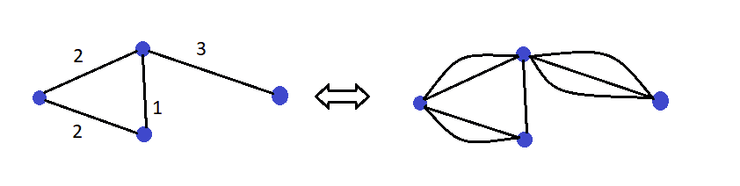
Multigrafo

É uma Rede onde as arestas estão associadas a valores naturais. Pode-se representar um multigrafo substituindo cada aresta por $n$ arestas, onde $n$ é o valor associado. (Com o exemplo fica claro)

Exemplo

NOTA

É normal referir-se a multigrafos como apenas grafos. O novo termo é só usado para evitar ambiguidade quando temos grafos e multigrafos.

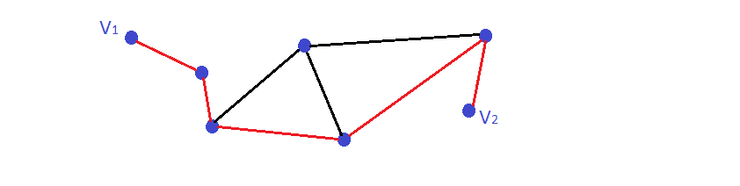
Caminho

Num grafo $g=(V,E)$ é uma sequência alternada de vértices e arestas $P = v_0a_1v_1\dots a_nv_n$ , onde $\forall j = 1,\dots,k$ , $a_j = v_{j-1}v_j$ , ou seja, cada aresta liga os vértices ao seu lado.

Atalho

Caminho que não repete arestas.

Trajetória

Caminho que não repete vértices, exceto no caso dos vértices inicial e final coincidirem. Neste caso a Trajetória é fechada, caso contrário é aberta.

Vértices Conectados

Dois vértices $u$ e $v$ de um grafo $g = (V,E)$ dizem-se conectados se forem o mesmo vértice ou se existir um caminho onde as extremidades são $u$ e $v$

Exemplo

$V_1$ e $V_2$ são vértices conectados.
O caminho vermelho é um exemplo de caminho que prova esse facto.

Grafo Conexo

Um grafo é conexo se quaisquer dois vértices do grafo estão conectados.

Subgrafo

Dado um grafo $g=(V,E)$ , diz-se que o grafo $h = (V',E')$ é subgrafo de $g$ se $V' \subseteq V$ ou $E'\subseteq E$ .
Um grafo é subgrafo de si mesmo

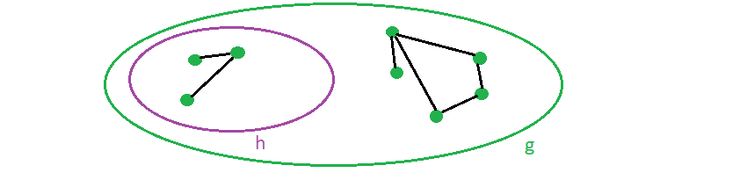
Componente

$h$ é uma componente de um grafo $g$ , se $h$ for um subgrafo conexo de $g$ e não for subgrafo de nenhum outro subgrafo conexo de $g$ .

Exemplo

$h$ é uma componente do grafo $g$

Grafo Planar

Grafo que é possível desenhar sem cruzar arestas.

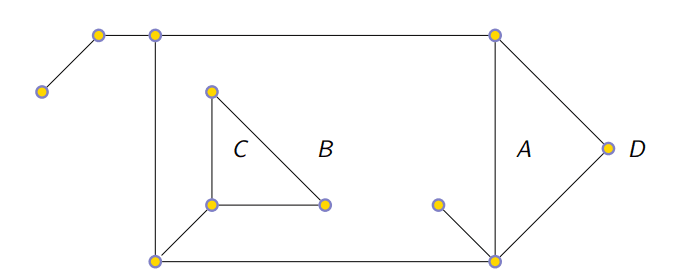
Teorema 3 - Lei de Euler

Seja $g$ um Grafo Planar, existe a seguinte relação:

\text{Arestas}+2=\text{Vértices}+\text{Regiões}

NOTA

A Região "Exterior" também conta

Exemplo

Sejam $A,B,C$ e $D$ as regiões, a igualdade confirma-se

13 + 2 = 11 + 4

Ponte

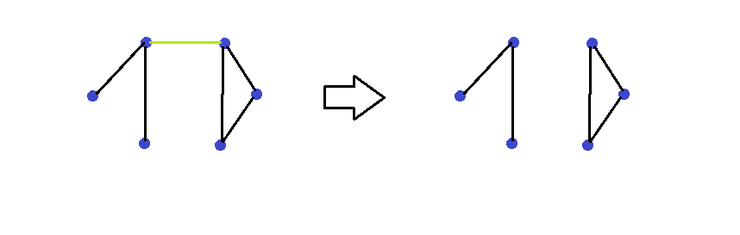
Aresta de um grafo, que, se for removida, aumenta o número de componentes.

Exemplo

A Aresta Verde é uma Ponte.

Teorema 4

Num grafo de $p$ vértices e $k$ componentes, o nº de arestas $(q)$ é tal que:

p-k\leq q \leq \frac{(p-k+1)(p-k)}{2}

Demonstração

Provar que $p-k \leq q$

Por indução simples, variando o Tamanho do Grafo $(q)$

$q=0$ ,
Neste caso o número de vértices é igual ao número de componentes.

0 \geq p-p = 0, \quad \text{P.V.}

Hipótese: Grafos com $q$ arestas (não importando o nº de componentes e vértices): $p-k \leq q$ .

Para esta prova, vamos supor que o grafo é esquelético, ou seja, todas as arestas são pontes. (No final da Demonstração há um exemplo de grafo esquelético.) Se a prova funcionar para grafos esqueléticos funcionará para qualquer um, pois estes têm o menor número de arestas para um dado número de vértices.

Se removermos uma aresta de um grafo esquelético, o número de componentes aumenta.
Deste modo, por hipótese de indução

q \geq p - k\quad \text{(Hip de Indução)}\\ q \geq p - (k+1)\quad \text{(Removendo uma aresta)}\\ q+1 \geq p-k

O que é válido, pois $q \geq p-k$ .
A primeira inequação está provada $\checkmark$ .

Provar que $q \leq \frac{(p-k+1)(p-k)}{2}$

Como estamos a tentar provar que o número de arestas tem um limite máximo, vamos ter em conta sempre os casos "máximos".

Seja $k'$ uma componente do grafo em estudo. Se essa componente tem $p'$ vértices, tem no máximo $\frac{p'(p'-1)}{2}$ arestas.

Se o grafo tem $k$ componentes, o que acontecerá se transferirmos um vértices de uma componente para outra?
Seja $h_1$ e $h_2$ duas componentes com $p_1, q_1$ e $p_2,q_2$ , respetivamente e $p_1 \leq p_2$ (o que é verdade para quaisquer duas componentes, haverá com mais vértices, ou têm as duas o mesmo número).
Seja $\Delta q_i, i=1,2$ a variação do número de arestas nas componentes $h_1$ e $h_2$ , quando "transferimos" um vértice de $h_1$ para $h_2$ .

\Delta q_1 = \frac{(p_1-1)(p_1-2)}{2}-\frac{p_1(p_1-1)}{2}\\ =1-p_1\\ \Delta q_2 = \frac{(p_2+1)p_2}{2}-\frac{p_2(p_2-1)}{2}\\ =p_2

A variação total será $1+p_2-p_1$ e será positiva pois $p_2 \geq p_1$

Assim, com o que acabamos de verificar, podemos concluir que um grafo com $k$ componentes terá o números máximo de arestas se e só se tem:

$k-1$ vértices isolados
$1$ componente com $p-(k-1)=p-k+1$ vértices

Nestas condições, o número máximo de arestas será:

\frac{(p-k+1)(p-k)}{2}

Finalmente, podemos concluir que $q\leq\frac{(p-k+1)(p-k)}{2}$
A segunda inequação está provada $\checkmark$ .

QED

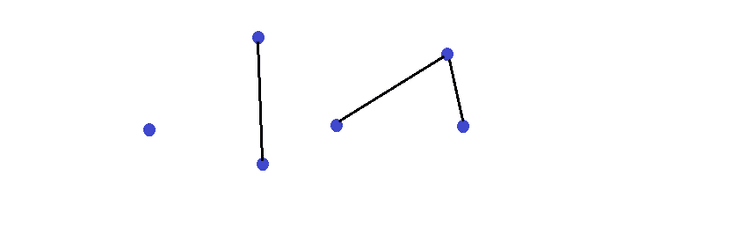
Exemplo Grafo Esquelético

Teorema 5

Se um grafo de $p$ vértices tem mais de $\frac{(p-1)(p-2)}{2}$ arestas, então é conexo.

Demonstração

Se o grafo não for convexo tem pelo menos $2$ componentes. Seja $q$ o número de arestas, pelo Teorema Anterior

q \leq \frac{(p-2+1)(p-2)}{2} = \frac{(p-1)(p-2)}{2}

Logo, como também vimos no Teorema Anterior que a "transferência" de vértices entre componentes aumenta $q$ , se passarmos todos os vértices de uma componente para outra (passando agora a ter apenas $1$ ), conclui-se que $q$ será maior do que a expressão acima.

QED