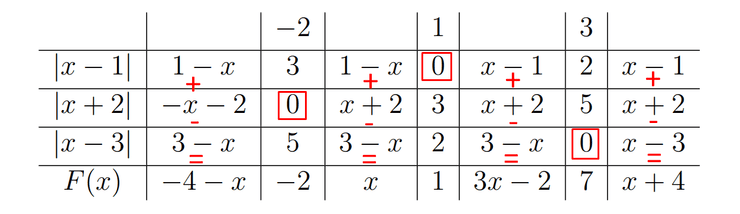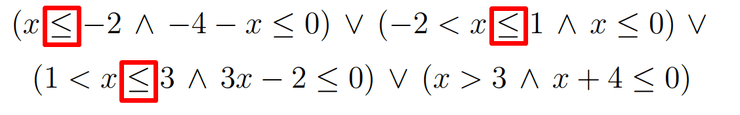Axiomática
Existem vários métodos de definir os números reais. No entanto, apenas vamos aprofundar no método que utiliza uma via axiomática e axiomas.
É importante perceber o que é um axioma antes de continuar.
TL;DR: Um axioma é uma afirmação que supomos ser verdadeira, e que a partir dela (ou de um conjunto de axiomas) vamos tirar conclusões, neste caso para chegar à definição de números reais.
Operação binária da soma
Uma operação binária é uma operação que tem dois operandos e um resultado.
- Axioma do fecho da adição
A qualquer operação que tenha a propriedade anteriormente estabelecida chama-se uma operação fechada em .
-
Axioma da associatividade da adição
-
Axioma da comutatividade da adição
tip
Nos PDFs em anexo, existem muitos mais exemplos de axiomas que são usados para definir o conjunto dos números reais. Na prática, esta informação não é assim tão importante, por isso o resumo disto acaba aqui :)
Inequações com somas/diferenças de módulos
Tomemos o exemplo seguinte:
Para resolver esta inequação, temos de utilizar uma tabela de módulos, atendendo aos pontos em que os módulos mudam de sinal. Assim, ficamos com os pontos .
É importante relembrar que quando se está a juntar as parcelas na linha não se pode esquecer dos sinais que estavam inicialmente na inequação. É de notar também a simetria da expressão após passar pelo seu zero.
Através da tabela anterior, podemos escrever a seguinte expressão:
É de salientar que não se pode esquecer de fechar os intervalos, isto é, de incluir os pontos de separação na tabela anterior (), exceto nos casos em que estes não fazem do domínio.
No final, ao resolver a expressão anterior, obtemos o resultado de .
PDFs: