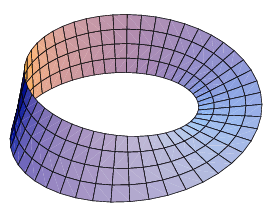
Uma superfície é orientável se tem uma normal definida continuamente que indica qual o "lado de dentro" e o "lado de fora" da superfície.
DEFINIÇÃO
Seja a superfície S ⊂ R 3 S \subset \R^3 S ⊂ R 3 S S S n ⃗ : S → R 3 \vec n: S \to \R^3 n : S → R 3
∀ x ∈ S \forall x \in S ∀ x ∈ S n ⃗ ( x ) ∈ ( T x S ) ⊥ \quad \vec n (x) \in (T_x S)^\perp n ( x ) ∈ ( T x S ) ⊥ ∣ ∣ n ⃗ ( x ) ∣ ∣ = 1 , ∀ x || \vec n (x) || = 1, \forall x ∣∣ n ( x ) ∣∣ = 1 , ∀ x n ⃗ \vec n n Como exemplo de uma superfície não orientável Fita de Möbius :
Também podemos ver um exemplo de uma superfície orientável
Teoremas:
Uma superfície descrita por uma parametrização é sempre orientável.
Uma superfície orientável tem sempre dois campos normais.
Demonstração Seja g : D ( u , v ) → S g: \underset{(u,v)}{D} \to S g : ( u , v ) D → S
T x S = L { colunas de D g } = L { ∂ g ∂ u , ∂ g ∂ v } T_x S = \mathcal{L} \{ \text{colunas de}\ Dg \} = \mathcal{L} \left\{ \frac{\partial g}{\partial u} , \frac{\partial g}{\partial v} \right\} T x S = L { colunas de D g } = L { ∂ u ∂ g , ∂ v ∂ g } ∂ g ∂ u × ∂ g ∂ v \frac{\partial g}{\partial u} \times \frac{\partial g}{\partial v} ∂ u ∂ g × ∂ v ∂ g ∂ g ∂ u e ∂ g ∂ v ⟹ ∂ g ∂ u × ∂ g ∂ v ∈ ( T x S ) ⊥ \frac{\partial g}{\partial u} \text{e} \frac{\partial g}{\partial v} \implies \frac{\partial g}{\partial u} \times \frac{\partial g}{\partial v} \in (T_x S)^{\perp} ∂ u ∂ g e ∂ v ∂ g ⟹ ∂ u ∂ g × ∂ v ∂ g ∈ ( T x S ) ⊥ Logo, n ⃗ ( x ) = ∂ g ∂ u × ∂ g ∂ v ∣ ∣ ∂ g ∂ u × ∂ g ∂ v ∣ ∣ \displaystyle \vec n (x) = \frac{\frac{\partial g}{\partial u} \times \frac{\partial g}{\partial v}}{|| \frac{\partial g}{\partial u} \times \frac{\partial g}{\partial v} ||} n ( x ) = ∣∣ ∂ u ∂ g × ∂ v ∂ g ∣∣ ∂ u ∂ g × ∂ v ∂ g 1 1 1
DEFINIÇÃO
Seja o campo vetorial F : R 3 → R 3 F: \R^3 \to \R^3 F : R 3 → R 3 S S S n ⃗ \vec n n
Definimos o fluxo de F F F S S S
∫ S F ⋅ n ⃗ = ∫ S F ( x , y , z ) ⋅ n ⃗ ( x , y , z ) \int_S F \cdot \vec n = \int_S F(x,y,z) \cdot \vec n (x,y,z) ∫ S F ⋅ n = ∫ S F ( x , y , z ) ⋅ n ( x , y , z ) Também se pode continuar a trabalhar a definição acima, para chegar a uma nova expressão para o fluxo:
∫ S F ⋅ n ⃗ = ∬ D F ( g ( u , v ) ) ⋅ ∂ g ∂ u × ∂ g ∂ v ∣ ∣ ∂ g ∂ u × ∂ g ∂ v ∣ ∣ ⋅ ∣ ∣ ∂ g ∂ u × ∂ g ∂ v ∣ ∣ d u d v = ∬ D F ( g ( u , v ) ) ⋅ ( ∂ g ∂ u × ∂ g ∂ v ) d u d v \begin{aligned}
\int_S F \cdot \vec n &= \iint_D F(g(u,v)) \cdot \frac{\frac{\partial g}{\partial u} \times \frac{\partial g}{\partial v}}{||\frac{\partial g}{\partial u} \times \frac{\partial g}{\partial v}||}
\cdot ||\frac{\partial g}{\partial u} \times \frac{\partial g}{\partial v}|| \d u \d v\\
&= \iint_D F(g(u,v)) \cdot \left(\frac{\partial g}{\partial u} \times \frac{\partial g}{\partial v}\right) \d u \d v
\end{aligned} ∫ S F ⋅ n = ∬ D F ( g ( u , v )) ⋅ ∣∣ ∂ u ∂ g × ∂ v ∂ g ∣∣ ∂ u ∂ g × ∂ v ∂ g ⋅ ∣∣ ∂ u ∂ g × ∂ v ∂ g ∣∣ d u d v = ∬ D F ( g ( u , v )) ⋅ ( ∂ u ∂ g × ∂ v ∂ g ) d u d v É também importante reforçar que, tal como anteriormente, o sinal do integral depende da orientação da parametrização.
Exemplo Sejam o campo vetorial F F F S S S
F ( x , y , z ) = ( x , y , z ) S = { x 2 + y 2 + z 2 = 1 , z > 0 } \begin{array}{ll}
F(x,y,z) = (x,y,z) &
S= \{x^2+y^2+z^2 = 1, z > 0 \}
\end{array} F ( x , y , z ) = ( x , y , z ) S = { x 2 + y 2 + z 2 = 1 , z > 0 } com orientação tal que, no ponto ( 0 , 1 , 0 ) (0,1,0) ( 0 , 1 , 0 ) n ⃗ \vec n n
Qual o fluxo de F F F S S S
Começamos por representar S S S
g ( u , v ) = ( sin v cos u , sin u sin v , cos v ) u ∈ ] 0 , 2 π [ , v ∈ ] 0 , π 2 [ \begin{aligned}
g(u, v) &= (\sin v \cos u, \sin u \sin v, \cos v)\\
&u \in ]0,2\pi[, v \in ]0, \frac{\pi}{2}[
\end{aligned} g ( u , v ) = ( sin v cos u , sin u sin v , cos v ) u ∈ ] 0 , 2 π [ , v ∈ ] 0 , 2 π [ ∂ g ∂ u = ( − sin u sin v , cos u sin v , 0 ) ∂ g ∂ v = ( cos v cos u , cos v sin u , − sin v ) \begin{aligned}
\frac{\partial g}{\partial u} &= (-\sin u \sin v, \cos u \sin v, 0)\\
\frac{\partial g}{\partial v} &= (\cos v \cos u, \cos v \sin u, -\sin v)
\end{aligned} ∂ u ∂ g ∂ v ∂ g = ( − sin u sin v , cos u sin v , 0 ) = ( cos v cos u , cos v sin u , − sin v ) De seguida calculamos o produto externo entre ∂ g ∂ u \frac{\partial g}{\partial u} ∂ u ∂ g ∂ g ∂ v \frac{\partial g}{\partial v} ∂ v ∂ g
∂ g ∂ u × ∂ g ∂ v = ∣ e 1 e 2 e 3 − sin u sin v cos u sin v 0 cos v cos u cos v sin u − sin v ∣ = ( − cos u sin 2 v , − sin u sin 2 v , − sin 2 u sin v cos v − cos 2 u sin v cos v ) = ( − cos u sin 2 v , − sin u sin 2 v , − sin v cos v ) \begin{aligned}
\frac{\partial g}{\partial u} \times \frac{\partial g}{\partial v} &= \begin{vmatrix}
e_1 & e_2 & e_3 \\
-\sin u \sin v & \cos u \sin v & 0\\
\cos v \cos u & \cos v \sin u & - \sin v
\end{vmatrix}\\
&= (-\cos u \sin^2 v, - \sin u \sin^2 v, - \sin^2 u \sin v \cos v - \cos^2 u \sin v \cos v)\\
&= (-\cos u \sin^2 v, - \sin u \sin^2 v, - \sin v \cos v)
\end{aligned} ∂ u ∂ g × ∂ v ∂ g = e 1 − sin u sin v cos v cos u e 2 cos u sin v cos v sin u e 3 0 − sin v = ( − cos u sin 2 v , − sin u sin 2 v , − sin 2 u sin v cos v − cos 2 u sin v cos v ) = ( − cos u sin 2 v , − sin u sin 2 v , − sin v cos v ) Temos de verificar agora se a orientação do campo é a correta.( 0 , 1 , 0 ) (0,1,0) ( 0 , 1 , 0 ) u = π 2 u = \frac{\pi}{2} u = 2 π v = π 2 v = \frac{\pi}{2} v = 2 π − sin u sin 2 v = − 1 < 0 -\sin u \sin^2 v = -1 < 0 − sin u sin 2 v = − 1 < 0 errada .
F ( g ( u , v ) ) = ( sin v cos u , sin u sin v , cos v ) F(g(u,v)) = (\sin v \cos u, \sin u \sin v, \cos v) F ( g ( u , v )) = ( sin v cos u , sin u sin v , cos v ) F ( g ( u , v ) ) ⋅ ( ∂ g ∂ u × ∂ g ∂ v ) = − cos 2 u sin 3 v − sin 2 u sin 3 v − sin v cos 2 v = − sin 3 v − sin v cos 2 v = − sin v \begin{aligned}
F(g(u,v)) \cdot \left(\frac{\partial g}{\partial u} \times \frac{\partial g}{\partial v}\right)
&= - \cos^2 u \sin^3 v - \sin^2 u \sin^3 v - \sin v \cos^2 v\\
&= - \sin^3 v - \sin v \cos^2 v\\
&= - \sin v
\end{aligned} F ( g ( u , v )) ⋅ ( ∂ u ∂ g × ∂ v ∂ g ) = − cos 2 u sin 3 v − sin 2 u sin 3 v − sin v cos 2 v = − sin 3 v − sin v cos 2 v = − sin v Assim, como a orientação está incorreta:
fluxo = − ∫ 0 2 π ∫ 0 π 2 ( − sin v ) d v d u = − ∫ 0 2 π [ cos v ] 0 π 2 d u = − ∫ 0 2 π − 1 d u = 2 π \begin{aligned}
\text{fluxo} &= - \int^{2\pi}_0 \int^{\frac{\pi}{2}}_0 (- \sin v) \d v \d u\\
&= - \int^{2 \pi}_0 [\cos v]^{\frac{\pi}{2}}_0 \d u\\
&= - \int^{2\pi}_0 - 1 \d u\\
&= 2\pi
\end{aligned} fluxo = − ∫ 0 2 π ∫ 0 2 π ( − sin v ) d v d u = − ∫ 0 2 π [ cos v ] 0 2 π d u = − ∫ 0 2 π − 1 d u = 2 π Alternativamente, podíamos ter usado a outra expressão para o fluxo, em que chegávamos a cálculos bastante mais simples:
Conseguimos "adivinhar" que o vetor normal é descrito por m ⃗ ( x , y , z ) = ( x , y , z ) \vec m (x,y,z) = (x,y,z) m ( x , y , z ) = ( x , y , z )
De seguida, é só calcular o fluxo:
F ⋅ m ⃗ = ( x , y , z ) ⋅ ( x , y , z ) = x 2 + y 2 + z 2 = 1 F \cdot \vec m = (x,y,z) \cdot (x,y,z) = x^2+ y^2+ z^2 = 1 F ⋅ m = ( x , y , z ) ⋅ ( x , y , z ) = x 2 + y 2 + z 2 = 1 Sabemos que a expressão acima é 1 visto que é uma (semi) esfera.
fluxo = ∫ S F ⋅ m ⃗ = ∫ S 1 d S = a ˊ rea ( S ) = 2 π \text{fluxo} = \int_S F \cdot \vec m = \int_S 1 \d S = \text{área}(S) = 2 \pi fluxo = ∫ S F ⋅ m = ∫ S 1 d S = a ˊ rea ( S ) = 2 π DEFINIÇÃO
Seja o campo vetorial F : R 3 → R 3 F : \R^3 \to \R^3 F : R 3 → R 3
div F = ∂ F 1 ∂ x + ∂ F 2 ∂ y + ∂ F 3 ∂ z \ondiv F = \frac{\partial F_1}{\partial x} + \frac{\partial F_2}{\partial y} + \frac{\partial F_3}{\partial z} div F = ∂ x ∂ F 1 + ∂ y ∂ F 2 + ∂ z ∂ F 3 Um domínio D ⊂ R 3 D \subset \R^3 D ⊂ R 3 domínio regular ∂ D \partial D ∂ D
DEFINIÇÃO
Seja D ⊂ R 3 D \subset \R^3 D ⊂ R 3 domínio regular n ⃗ \vec n n ∂ D \partial D ∂ D D D D
∫ ∂ D F ⋅ n ⃗ = ∭ D div F \int_{\partial D} F \cdot \vec n = \iiint_D \ondiv F ∫ ∂ D F ⋅ n = ∭ D div F Exemplo Sejam o campo vetorial F F F S S S
F ( x , y , z ) = ( x , y , − 2 z ) S = { x 2 + y 2 = 1 + 2 z 2 , 0 ≤ z ≤ 1 } \begin{aligned}
F(x,y,z) &= (x,y, -2z)\\
S &= \{x^2+y^2 = 1 + 2z^2, 0 \leq z \leq 1 \}
\end{aligned} F ( x , y , z ) S = ( x , y , − 2 z ) = { x 2 + y 2 = 1 + 2 z 2 , 0 ≤ z ≤ 1 } em que S S S
Qual o valor de ∫ S F ⋅ n ⃗ \int_S F \cdot \vec n ∫ S F ⋅ n
div F = 1 + 1 − 2 = 0 \ondiv F = 1+1-2 = 0 div F = 1 + 1 − 2 = 0
D = { x 2 + y 2 ≤ 1 + 2 z 2 , 0 ≤ z ≤ 1 } D = \{ x^2+y^2 \leq 1 + 2 z^2, 0 \leq z \leq 1 \} D = { x 2 + y 2 ≤ 1 + 2 z 2 , 0 ≤ z ≤ 1 } ∂ D = \partial D = ∂ D = ( S ) (S) ( S ) ( T 1 , z = 1 ) (T_1, z=1) ( T 1 , z = 1 ) ( T 0 , z = 0 ) (T_0, z=0) ( T 0 , z = 0 )
Pelo teorema da divergência:
∫ ∂ D F ⋅ n ⃗ e x t = ∭ D div F = 0 \int_{\partial D} F \cdot \vec n_{ext} = \iiint_D \ondiv F = 0 ∫ ∂ D F ⋅ n e x t = ∭ D div F = 0 ∫ ∂ D F ⋅ n ⃗ e x t = ∫ S F ⋅ n ⃗ e x t + ∫ T 1 F ⋅ n ⃗ e x t + ∫ T 2 F ⋅ n ⃗ e x t ⟹ ∫ S F ⋅ n ⃗ e x t = − ∫ T 1 F ⋅ n ⃗ e x t − ∫ T 2 F ⋅ n ⃗ e x t \begin{darray}{l}
\int_{\partial D} F \cdot \vec n_{ext} = \int_S F \cdot \vec n_{ext} + \int_{T_1} F \cdot \vec n_{ext} + \int_{T_2} F \cdot \vec n_{ext}\\
\implies \int_S F \cdot \vec n_{ext} = - \int_{T_1} F \cdot \vec n_{ext} - \int_{T_2} F \cdot \vec n_{ext}
\end{darray} ∫ ∂ D F ⋅ n e x t = ∫ S F ⋅ n e x t + ∫ T 1 F ⋅ n e x t + ∫ T 2 F ⋅ n e x t ⟹ ∫ S F ⋅ n e x t = − ∫ T 1 F ⋅ n e x t − ∫ T 2 F ⋅ n e x t Em T 1 T_1 T 1 n ⃗ e x t = ( 0 , 0 , 1 ) \vec n_{ext} = (0,0,1) n e x t = ( 0 , 0 , 1 ) F ⋅ n ⃗ e x t = − 2 z F \cdot \vec n_{ext} = -2z F ⋅ n e x t = − 2 z z = 1 z=1 z = 1
∫ T 1 − 2 z d S = ∫ T 1 − 2 d S = − 2 × a ˊ rea ( T 1 ) = − 2 × 3 π = − 6 π \int_{T_1} - 2z \d S = \int_{T_1} - 2 \d S = -2 \times \text{área}(T_1) = -2 \times 3 \pi = -6\pi ∫ T 1 − 2 z d S = ∫ T 1 − 2 d S = − 2 × a ˊ rea ( T 1 ) = − 2 × 3 π = − 6 π Em T 0 T_0 T 0 n ⃗ e x t = ( 0 , 0 , − 1 ) \vec n_{ext} = (0,0,-1) n e x t = ( 0 , 0 , − 1 ) F ⋅ n ⃗ e x t = 2 z F \cdot \vec n_{ext} = 2z F ⋅ n e x t = 2 z z = 0 z=0 z = 0
∫ T 0 F ⋅ n ⃗ e x t d S = 0 \int_{T_0} F \cdot \vec n_{ext} \d S = 0 ∫ T 0 F ⋅ n e x t d S = 0 ∫ S F ⋅ n ⃗ e x t = − ( − 6 π ) − 0 = 6 π \int_S F \cdot \vec n_{ext} = -(-6\pi ) - 0 = 6 \pi ∫ S F ⋅ n e x t = − ( − 6 π ) − 0 = 6 π Considerando um campo vetorial F F F
F : R 3 → R 3 , C 1 , x 0 ∈ R 3 F: \R^3 \to \R^3, C^1, x_0 \in \R^3 F : R 3 → R 3 , C 1 , x 0 ∈ R 3 ∫ ∂ B ϵ ( x 0 ) F ⋅ n ⃗ = ∫ ∂ B ϵ ( x 0 ) div F ≈ div F ( x 0 ) ⋅ ∫ ∂ B ϵ ( x 0 ) 1 = div F ( x 0 ) ⋅ volume ( B ϵ ( x 0 ) ) \int_{\partial B_{\epsilon} (x_0)} F \cdot \vec n = \int_{\partial B_{\epsilon} (x_0)} \ondiv F \approx \ondiv F(x_0) \cdot \int_{\partial B_{\epsilon} (x_0)} 1
= \ondiv F(x_0) \cdot \text{volume}(B_{\epsilon} (x_0)) ∫ ∂ B ϵ ( x 0 ) F ⋅ n = ∫ ∂ B ϵ ( x 0 ) div F ≈ div F ( x 0 ) ⋅ ∫ ∂ B ϵ ( x 0 ) 1 = div F ( x 0 ) ⋅ volume ( B ϵ ( x 0 )) div F ( x 0 ) = lim ϵ → 0 1 vol ( B ϵ ( x 0 ) ) ∫ ∂ B ϵ ( x 0 ) F ⋅ n ⃗ \ondiv_F(x_0) = \lim_{\epsilon \to 0} \frac{1}{\text{vol}(B_{\epsilon} (x_0))} \int_{\partial B_{\epsilon} (x_0)} F \cdot \vec n div F ( x 0 ) = ϵ → 0 lim vol ( B ϵ ( x 0 )) 1 ∫ ∂ B ϵ ( x 0 ) F ⋅ n
Se div F ( x 0 ) > 0 \ondiv F(x_0) > 0 div F ( x 0 ) > 0 ∫ ∂ B ϵ ( x 0 ) F ⋅ n ⃗ > 0 \int_{\partial B_{\epsilon} (x_0)} F \cdot \vec n > 0 ∫ ∂ B ϵ ( x 0 ) F ⋅ n > 0 x 0 x_0 x 0
Se div F ( x 0 ) < 0 \ondiv F(x_0) < 0 div F ( x 0 ) < 0 ∫ ∂ B ϵ ( x 0 ) F ⋅ n ⃗ < 0 \int_{\partial B_{\epsilon} (x_0)} F \cdot \vec n < 0 ∫ ∂ B ϵ ( x 0 ) F ⋅ n < 0 x 0 x_0 x 0
Se div F ( x 0 ) = 0 \ondiv F(x_0) = 0 div F ( x 0 ) = 0 x 0 x_0 x 0
Slides: