Um intervalo aberto de R n \R^n R n
I = ] a 1 , b 1 [ × ] a 2 , b 2 [ × ⋯ × ] a n , b n [ I = ]a_1, b_1[ \times ]a_2, b_2[ \times \dots \times ]a_n, b_n[ I = ] a 1 , b 1 [ × ] a 2 , b 2 [ × ⋯ × ] a n , b n [
Por exemplo, em R 2 \R^2 R 2 R 3 \R^3 R 3
Podemos também calcular o comprimento, área, volume, etc através de um intervalo.
∣ I ∣ = ( b 1 − a 1 ) × ( b 2 − a 2 ) × ⋯ × ( b n − a n ) |I| = (b_1-a_1) \times (b_2-a_2)\times \dots \times (b_n-a_n) ∣ I ∣ = ( b 1 − a 1 ) × ( b 2 − a 2 ) × ⋯ × ( b n − a n )
Em R \R R ∣ I ∣ |I| ∣ I ∣
Em R 2 \R^2 R 2 ∣ I ∣ |I| ∣ I ∣
Em R 3 \R^3 R 3 ∣ I ∣ |I| ∣ I ∣
Uma partição de I I I
Dada uma partição, uma função em escada nessa partição é uma função que é constante em cada subintervalo.
Uma propriedade das funções em escada é que é muito fácil calcular o seu integral.
Em geral, se f : I → R f: I \to \R f : I → R
∫ I f = ∑ J elemento da parti c ¸ a ˜ o ( valor da fun c ¸ a ˜ o ) × ∣ J ∣ \int_I f= \sum_{J\text{ elemento da partição}} (\text{valor da função}) \times |J| ∫ I f = ∑ J elemento da parti c ¸ a ˜ o ( valor da fun c ¸ a ˜ o ) × ∣ J ∣
Exemplo
Em R \R R
∫ 0 8 = 3 × 1 + 2 × 2 + 4 × 2 + 1 × 3 = 3 + 4 + 8 + 3 = 18 \int^8_0=3\times 1 + 2\times 2 + 4\times 2 + 1\times 3 = 3+4+8+3 = 18 ∫ 0 8 = 3 × 1 + 2 × 2 + 4 × 2 + 1 × 3 = 3 + 4 + 8 + 3 = 18
Em geral, se, f : I → R f: I \to \R f : I → R ∫ I f \int_I f ∫ I f
"∫ I f ≤ \int_I f \leq ∫ I f ≤
"∫ I f ≥ \int_I f \geq ∫ I f ≥
DEFINIÇÃO
Integral superior de f f f
∫ I f ≤ ∫ I ‾ f = inf { Integrais de todas as fun c ¸ o ˜ es em cada subintervalo por excesso } \int_I f \leq \overline{\int_I} f = \operatorname{inf} \{\text{Integrais de todas as funções em cada subintervalo por excesso}\} ∫ I f ≤ ∫ I f = inf { Integrais de todas as fun c ¸ o ˜ es em cada subintervalo por excesso }
Integral inferior de f f f
∫ I f ≥ ∫ I ‾ f = sup { Integrais de todas as fun c ¸ o ˜ es em cada subintervalo por defeito } \int_I f \geq \underline{\int_I} f = \operatorname{sup} \{\text{Integrais de todas as funções em cada subintervalo por defeito}\} ∫ I f ≥ ∫ I f = sup { Integrais de todas as fun c ¸ o ˜ es em cada subintervalo por defeito }
Assim, conseguimos obter a definição de função integrável.
DEFINIÇÃO
f : I → R f: I \to \R f : I → R ∫ ‾ I f = ∫ ‾ I f \overline{\int}_I f=\underline{\int}_I f ∫ I f = ∫ I f
∫ I f : = ∫ I ‾ f ( ou ∫ I ‾ f ) \int_I f := \overline{\int_I} f \left(\text{ou} \underline{\int_I} f\right) ∫ I f := ∫ I f ( ou ∫ I f )
Se f , g : I → R f, g: I \to \R f , g : I → R
∫ I ( a f + b g ) = a ∫ I f + b ∫ I g , a , b ∈ R \int_I (af+bg) = a\int_I f + b\int_I g, \quad a,b\in \R ∫ I ( a f + b g ) = a ∫ I f + b ∫ I g , a , b ∈ R
Se f ≤ g f \leq g f ≤ g ∫ I f ≤ ∫ I g \int_I f \leq \int_I g ∫ I f ≤ ∫ I g
Se I 1 ∪ I 2 I_1 \cup I_2 I 1 ∪ I 2 I I I
∫ I f = ∫ I 1 f + ∫ I 2 f \int_I f= \int_{I_1} f + \int_{I_2} f ∫ I f = ∫ I 1 f + ∫ I 2 f
Este teorema permite-nos calcular o valor de integrais em intervalos de d i m > 1 dim > 1 d im > 1
DEFINIÇÃO
Se f : I → R f: I \to \R f : I → R I I I R n \R^n R n I = ] a 1 , b 1 [ × ⋯ × ] a n , b n [ I = ]a_1,b_1[ \times \dots \times ]a_n,b_n[ I = ] a 1 , b 1 [ × ⋯ × ] a n , b n [
∫ I f = ∫ a n b n ( ∫ a n − 1 b n − 1 … ( ∫ a 1 b 1 f ( x ) d x 1 ) … d x n − 1 ) d x n \int_I f= \int^{b_n}_{a_n} \left( \int^{b_{n-1}}_{a_{n-1}} \dots \left(\int^{b_1}_{a_1} f(x) \d x_1 \right) \dots \d x_{n-1} \right) \d x_n ∫ I f = ∫ a n b n ( ∫ a n − 1 b n − 1 … ( ∫ a 1 b 1 f ( x ) d x 1 ) … d x n − 1 ) d x n warning
Não interessa a ordem das variáveis no contexto deste Teorema.
As expressões abaixo são equivalentes, considerando
I = ] 0 , 1 [ × ] 2 , 3 [ I = ]0, 1[\times ] 2, 3[ I = ] 0 , 1 [ × ] 2 , 3 [
∫ I f = ∫ 0 1 ( ∫ 2 3 f d y ) d x = ∫ 2 3 ( ∫ 0 1 f d x ) d y \int_I f = \int^1_0 \left(\int^3_2 f \d y\right)\d x = \int^3_2 \left( \int^1_0 f \d x\right)\d y ∫ I f = ∫ 0 1 ( ∫ 2 3 f d y ) d x = ∫ 2 3 ( ∫ 0 1 f d x ) d y
Exemplos Considerando
I = ] 0 , 1 [ × ] 0 , 1 [ e f ( x , y ) = x ( x 2 + y ) 2 \begin{array}{l c l}
I = ]0, 1[ \times ]0, 1[ & \text{e} & f(x,y) = x(x^2+y)^2
\end{array} I = ] 0 , 1 [ × ] 0 , 1 [ e f ( x , y ) = x ( x 2 + y ) 2 calcule o integral de f f f I I I
∫ I f = ∫ 0 1 ( ∫ 0 1 f ( x , y ) d x ) d y = ∫ 0 1 ( ∫ 0 1 x ( x 2 + y ) 2 d x ) d y = 1 2 ∫ 0 1 ( ∫ 0 1 2 x ( x 2 + y ) 2 d x ) d y = 1 2 ∫ 0 1 [ ( x 2 + y ) 3 3 ] 0 1 d y = 1 2 ∫ 0 1 ( ( 1 + y ) 3 3 − y 3 3 ) d y = 1 2 [ ( 1 + y ) 4 3 × 4 − y 4 3 × 4 ] 0 1 = 1 2 ( ( 2 4 12 − 1 12 ) − ( 1 12 − 0 ) ) = 1 2 ⋅ 14 12 = 7 12 \begin{aligned}
\int_I f &= \int^1_0 \left( \int^1_0 f(x,y) \d x\right) \d y \\
&= \int^1_0\left(\int^1_0 x(x^2+y)^2 \d x\right) \d y\\
&= \frac 12 \int^1_0 \left( \int^1_0 2x(x^2+y)^2 \d x\right) \d y \\
&= \frac 12 \int^1_0 \left[\frac{ \left(x^2+y\right)^3}{3}\right]^1_0 \d y\\
&= \frac 12 \int^1_0 \left( \frac{\left(1+y\right)^3}{3} - \frac{y^3}{3}\right)\d y \\
&= \frac 12 \left[\frac{\left(1+y\right)^4}{3\times 4} - \frac{y^4}{3\times 4}\right]^1_0\\
&= \frac 12 \left(\left(\frac{2^4}{12}- \frac{1}{12}\right)-\left(\frac{1}{12} - 0\right)\right)\\
&= \frac{1}{2} \cdot \frac{14}{12}\\
&= \frac{7}{12}\\
\end{aligned} ∫ I f = ∫ 0 1 ( ∫ 0 1 f ( x , y ) d x ) d y = ∫ 0 1 ( ∫ 0 1 x ( x 2 + y ) 2 d x ) d y = 2 1 ∫ 0 1 ( ∫ 0 1 2 x ( x 2 + y ) 2 d x ) d y = 2 1 ∫ 0 1 [ 3 ( x 2 + y ) 3 ] 0 1 d y = 2 1 ∫ 0 1 ( 3 ( 1 + y ) 3 − 3 y 3 ) d y = 2 1 [ 3 × 4 ( 1 + y ) 4 − 3 × 4 y 4 ] 0 1 = 2 1 ( ( 12 2 4 − 12 1 ) − ( 12 1 − 0 ) ) = 2 1 ⋅ 12 14 = 12 7 Considerando
I = ] 0 , 1 [ × ] 0 , 2 [ e f ( x , y ) = { x 3 y se x 2 < y < 2 x 2 0 c.c. \begin{array}{l c l}
I = ]0,1[ \times ]0, 2[
&\text{e}
&
f(x,y) =
\begin{cases}
x^3y & \text{se } x^2 < y <2x^2\\
0 & \text{c.c.}
\end{cases}
\end{array} I = ] 0 , 1 [ × ] 0 , 2 [ e f ( x , y ) = { x 3 y 0 se x 2 < y < 2 x 2 c.c. calcule o integral de f f f I I I
∫ I f = ∫ 0 1 ( ∫ 0 2 f ( x , y ) d y ) d x = ∫ 0 1 ( ∫ x 2 2 x 2 x 3 y d y ) d x = ∫ 0 1 [ x 3 y 2 2 ] x 2 2 x 2 d x = ∫ 0 1 ( x 3 ( 2 x 2 ) 2 2 − x 3 ( x 2 ) 2 2 ) d x = ∫ 0 1 2 x 7 − x 7 2 d x = ∫ 0 1 3 2 x 7 d x = 3 2 [ x 8 8 ] 0 1 = 3 2 ⋅ ( 1 8 − 0 ) = 3 16 \begin{aligned}
\int_I f &= \int^1_0 \left(\int^2_0 f\left(x,y\right) \d y\right)\d x \\
&= \int^1_0 \left(\int^{2x^2}_{x^2} x^3 y \d y\right)\d x\\
&=\int^1_0 \left[x^3 \frac{y^2}{2}\right]^{2x^2}_{x^2} \d x \\
&= \int^1_0 \left(x^3\frac{\left(2x^2\right)^2}{2} - \frac{x^3\left(x^2\right)^2}{2}\right) \d x\\
&=\int^1_0 2x^7 - \frac{x^7}{2} \d x \\
&= \int^1_0 \frac{3}{2} x^7 \d x \\
&= \frac{3}{2} \left[\frac{x^8}{8}\right]^1_0\\
&=\frac{3}{2} \cdot \left(\frac{1}{8} - 0\right) \\
&= \frac{3}{16}\\
\end{aligned} ∫ I f = ∫ 0 1 ( ∫ 0 2 f ( x , y ) d y ) d x = ∫ 0 1 ( ∫ x 2 2 x 2 x 3 y d y ) d x = ∫ 0 1 [ x 3 2 y 2 ] x 2 2 x 2 d x = ∫ 0 1 ( x 3 2 ( 2 x 2 ) 2 − 2 x 3 ( x 2 ) 2 ) d x = ∫ 0 1 2 x 7 − 2 x 7 d x = ∫ 0 1 2 3 x 7 d x = 2 3 [ 8 x 8 ] 0 1 = 2 3 ⋅ ( 8 1 − 0 ) = 16 3 Porquê integrar primeiro em y y y x x x Porque simplifica os cálculos.
Ambas as estratégias irão chegar à resposta correta, mas como podemos ver pela expressão abaixo,
teríamos de calcular o valor de dois integrais e não um.
∫ 0 1 ( ∫ y 2 y f ( x , y ) d x ) d y + ∫ 1 2 ( ∫ y 2 1 f ( x , y ) d x ) d y \int^1_0 \left( \int^{\sqrt{y}}_{\frac{\sqrt{y}}{2}} f\left(x,y\right) \d x\right)\d y + \int^2_1 \left( \int^1_{\frac{\sqrt y}{2}} f\left(x,y\right) \d x\right) \d y ∫ 0 1 ( ∫ 2 y y f ( x , y ) d x ) d y + ∫ 1 2 ( ∫ 2 y 1 f ( x , y ) d x ) d y Este teorema permite-nos concluir a relação entre os integrais e o comprimento, área e volume.
a ˊ rea = ∫ comprimento \text{área} = \int \text{comprimento} a ˊ rea = ∫ comprimento volume = ∫ a ˊ rea \text{volume} = \int \text{área} volume = ∫ a ˊ rea
Expandindo a definição de área, chegamos à função 1 l \1 1 l
a ˊ rea = ∫ a b comprimento ( x ) d x = ∫ a b ( f ( x ) − g ( x ) ) d x = ∫ a b ( ∫ g ( x ) f ( x ) 1 d y ) d x = ∫ 1 l A ( x , y ) d x d y \begin{aligned}
\text{área} &= \int^b_a \text{comprimento} (x) \d x \\
&= \int^b_a\left(f(x)-g(x)\right) \d x\\
&= \int^b_a\left(\int^{f(x)}_{g(x)} 1 \d y\right) \d x\\
&= \int \1_A (x,y) \d x \d y
\end{aligned} a ˊ rea = ∫ a b comprimento ( x ) d x = ∫ a b ( f ( x ) − g ( x ) ) d x = ∫ a b ( ∫ g ( x ) f ( x ) 1 d y ) d x = ∫ 1 l A ( x , y ) d x d y 1 l A = { 1 , ( x , y ) ∈ A 0 , ( x , y ) ∉ A \1_A =
\begin{cases}
1&,&(x,y) \in A\\
0&,&(x,y)\notin A
\end{cases} 1 l A = { 1 0 , , ( x , y ) ∈ A ( x , y ) ∈ / A DEFINIÇÃO
Assim, podemos definir o volume n-dimensional de um conjunto A A A
∫ 1 l A em que 1 l A = { 1 , ( x , y ) ∈ A 0 , ( x , y ) ∉ A \begin{array}{l l l}
\int \1_A
& \text{em que}
&
\1_A =
\begin{cases}
1&,&(x,y) \in A\\
0&,&(x,y)\notin A
\end{cases}
\end{array} ∫ 1 l A em que 1 l A = { 1 0 , , ( x , y ) ∈ A ( x , y ) ∈ / A Exemplos Qual o volume do conjunto abaixo?
{ x > 0 , y > 0 , z > 0 , x + y + z < 1 } \{x> 0, y> 0, z > 0, x+y+z<1\} { x > 0 , y > 0 , z > 0 , x + y + z < 1 } Neste tipo de exercícios, podemos escolher que variável devemos fixar primeiro.Esta escolha é muito importante porque nos pode simplificar bastante os cálculos, se escolhermos a variável certa.
Volume = ∫ 0 1 A ˊ rea ( z ) d z \text{Volume} = \int^1_0 \text{Área}(z) \d z Volume = ∫ 0 1 A ˊ rea ( z ) d z
Fixado z z z
Restri c ¸ o ˜ es na figura: { x > 0 y > 0 x + y < 1 − z \text{Restrições na figura: }
\begin{cases}
x>0\\
y>0\\
x+y<1-z
\end{cases} Restri c ¸ o ˜ es na figura: ⎩ ⎨ ⎧ x > 0 y > 0 x + y < 1 − z A ˊ rea = ∫ 0 1 − z ( ∫ 0 1 − z − x 1 d y ) d x \text{Área} = \int^{1-z}_0\left(\int^{1-z-x}_0 1 \d y\right) \d x A ˊ rea = ∫ 0 1 − z ( ∫ 0 1 − z − x 1 d y ) d x Volume = ∫ 0 1 ( ∫ 0 1 − z ( ∫ 0 1 − z − x 1 d y ) d x ) d z = ∫ 0 1 ( ∫ 0 1 − z ( 1 − z − x ) d x ) d z = ∫ 0 1 [ ( 1 − z ) x − x 2 2 ] 0 1 − z d z = ∫ 0 1 ( ( 1 − z ) 2 − ( 1 − z ) 2 2 − 0 ) d z = ∫ 0 1 ( 1 − z ) 2 2 d z = [ − ( 1 − z ) 3 6 ] 0 1 = 0 − ( − 1 6 ) = 1 6 \begin{aligned}
\text{Volume} &= \int^1_0 \left(\int^{1-z}_0\left(\int^{1-z-x}_0 1 \d y\right) \d x\right) \d z\\
&=\int^1_0 \left(\int^{1-z}_0\left(1-z-x\right) \d x\right) \d z\\
&=\int^1_0 \left[\left(1-z\right)x - \frac{x^2}{2}\right]^{1-z}_0 \d z\\
&=\int^1_0 \left(\left(1-z\right)^2 - \frac{\left(1-z\right)^2}{2} - 0\right) \d z \\
&=\int^1_0 \frac{\left(1-z\right)^2}{2} \d z\\
&= \left[-\frac{\left(1-z\right)^3}{6}\right]^1_0\\
&= 0 - \left(-\frac{1}{6}\right) \\
&= \frac{1}{6}
\end{aligned} Volume = ∫ 0 1 ( ∫ 0 1 − z ( ∫ 0 1 − z − x 1 d y ) d x ) d z = ∫ 0 1 ( ∫ 0 1 − z ( 1 − z − x ) d x ) d z = ∫ 0 1 [ ( 1 − z ) x − 2 x 2 ] 0 1 − z d z = ∫ 0 1 ( ( 1 − z ) 2 − 2 ( 1 − z ) 2 − 0 ) d z = ∫ 0 1 2 ( 1 − z ) 2 d z = [ − 6 ( 1 − z ) 3 ] 0 1 = 0 − ( − 6 1 ) = 6 1 Qual o volume do conjunto abaixo?
S = { ( x , y ) ∈ R 2 , y > x 2 , y < 1 − x 2 } S=\{(x,y) \in \R^2, y> x^2, y < 1-x^2\} S = {( x , y ) ∈ R 2 , y > x 2 , y < 1 − x 2 } Fixando primeiro x x x
{ y = x 2 y = 1 − x 2 ⇔ { 1 − x 2 = x 2 y = x 2 ⇔ 1 = 2 x 2 ⇔ x = ± 2 2 \begin{cases}
y=x^2\\
y=1-x^2
\end{cases}
\Leftrightarrow
\begin{cases}
1-x^2= x^2\\
y=x^2
\end{cases}
\Leftrightarrow
1=2x^2
\Leftrightarrow
x=\pm \frac{\sqrt 2}{2} { y = x 2 y = 1 − x 2 ⇔ { 1 − x 2 = x 2 y = x 2 ⇔ 1 = 2 x 2 ⇔ x = ± 2 2 A ˊ rea = ∫ − 2 2 2 2 ( ∫ x 2 1 − x 2 1 d y ) d x = ∫ − 2 2 2 2 1 − x 2 − x 2 d x = ∫ − 2 2 2 2 1 − 2 x 2 d x = [ x − 2 x 3 3 ] − 2 2 2 2 = 2 2 − 2 2 2 8 3 − ( − 2 2 − 2 ( − 2 2 8 ) 3 ) = 2 2 − 2 6 + 2 2 − 2 6 = 2 2 3 \begin{aligned}
\text{Área} &= \int^{\frac{\sqrt 2}{2}}_{-\frac{\sqrt 2}{2}} \left(\int^{1-x^2}_{x^2} 1 \d y\right)\d x\\
&=\int^{\frac{\sqrt 2}{2}}_{-\frac{\sqrt 2}{2}} 1-x^2-x^2 \d x\\
&=\int^{\frac{\sqrt 2}{2}}_{-\frac{\sqrt 2}{2}} 1-2x^2 \d x\\
&=\left[x-\frac{2x^3}{3}\right]^{\frac{\sqrt 2}{2}}_{-\frac{\sqrt 2}{2}}\\
&=\frac{\sqrt 2}{2} - \frac{2 \frac{2\sqrt 2}{8}}{3} - \left(-\frac{\sqrt 2}{2} - \frac{2 \left( -\frac{2\sqrt 2}{8}\right)}{3}\right)\\
&=\frac{\sqrt 2}{2} - \frac{\sqrt 2}{6} +\frac{\sqrt 2}{2} - \frac{\sqrt 2}{6}\\
&=\frac{2\sqrt{2}}{3}
\end{aligned} A ˊ rea = ∫ − 2 2 2 2 ( ∫ x 2 1 − x 2 1 d y ) d x = ∫ − 2 2 2 2 1 − x 2 − x 2 d x = ∫ − 2 2 2 2 1 − 2 x 2 d x = [ x − 3 2 x 3 ] − 2 2 2 2 = 2 2 − 3 2 8 2 2 − − 2 2 − 3 2 ( − 8 2 2 ) = 2 2 − 6 2 + 2 2 − 6 2 = 3 2 2 No entanto, podíamos tentar fixar primeiro y y y
Chegamos sempre à mesma resposta , com qualquer um dos métodos.
Então, fixando primeiro y y y
∫ 0 1 comprimento ( y ) d y \int^1_0 \text{comprimento}(y) \d y ∫ 0 1 comprimento ( y ) d y
Se 0 < y < 1 2 0 < y < \frac{1}{2} 0 < y < 2 1 y = x 2 ⇒ x = ± y y = x^2 \Rightarrow x = \pm \sqrt{y} y = x 2 ⇒ x = ± y comprimento ( y ) = ∫ − y y 1 d x \text{comprimento}(y) = \int^{\sqrt{y}}_{-\sqrt{y}} 1 \d x comprimento ( y ) = ∫ − y y 1 d x
Se 1 2 < y < 1 \frac{1}{2} < y < 1 2 1 < y < 1 y = 1 − x 2 ⇒ x = ± 1 − y y = 1 - x^2 \Rightarrow x = \pm \sqrt{1-y} y = 1 − x 2 ⇒ x = ± 1 − y comprimento ( y ) = ∫ − 1 − y 1 − y 1 d x \text{comprimento}(y) = \int^{\sqrt{1-y}}_{-\sqrt{1-y}} 1 \d x comprimento ( y ) = ∫ − 1 − y 1 − y 1 d x
A ˊ rea = ∫ 0 1 2 ( ∫ − y y 1 d x ) d y + ∫ 1 2 1 ( ∫ − 1 − y 1 − y 1 d x ) d y = ∫ 0 1 2 ( 2 y ) d y + ∫ 1 2 1 ( 2 1 − y ) d y = [ 2 y 3 2 3 2 ] 0 1 2 + [ − 2 ( 1 − y ) 3 2 3 2 ] 1 2 1 = ( 2 ⋅ 2 3 ⋅ ( 1 2 ) 3 2 − 0 ) + ( 0 − ( − 2 ⋅ 2 3 ⋅ ( 1 2 ) 3 2 ) ) = 4 3 ⋅ 1 2 2 + 4 3 ⋅ 1 2 2 = 2 3 2 + 2 3 2 = 2 2 3 \begin{aligned}
\text{Área} & =\int _{0}^{\frac{1}{2}}\left(\int _{-\sqrt{y}}^{\sqrt{y}} 1\d x\right) \d y+\int _{\frac{1}{2}}^{1}\left(\int _{-\sqrt{1-y}}^{\sqrt{1-y}} 1\d x\right) \d y\\
& =\int _{0}^{\frac{1}{2}}\left( 2\sqrt{y}\right) \d y+\int _{\frac{1}{2}}^{1}\left( 2\sqrt{1-y}\right) \d y\\
& =\left[\frac{2y^{\frac{3}{2}}}{\frac{3}{2}}\right]_{0}^{\frac{1}{2}} +\left[ -\frac{2( 1-y)^{\frac{3}{2}}}{\frac{3}{2}}\right]_{\frac{1}{2}}^{1}\\
& =\left( 2\cdot \frac{2}{3} \cdot \left(\frac{1}{2}\right)^{\frac{3}{2}} -0\right) +\left( 0-\left( -2\cdot \frac{2}{3} \cdot \left(\frac{1}{2}\right)^{\frac{3}{2}}\right)\right)\\
& =\frac{4}{3} \cdot \frac{1}{2\sqrt{2}} +\frac{4}{3} \cdot \frac{1}{2\sqrt{2}}\\
& =\frac{2}{3\sqrt{2}} +\frac{2}{3\sqrt{2}}\\
& =\frac{2\sqrt{2}}{3}
\end{aligned} A ˊ rea = ∫ 0 2 1 ( ∫ − y y 1 d x ) d y + ∫ 2 1 1 ( ∫ − 1 − y 1 − y 1 d x ) d y = ∫ 0 2 1 ( 2 y ) d y + ∫ 2 1 1 ( 2 1 − y ) d y = [ 2 3 2 y 2 3 ] 0 2 1 + [ − 2 3 2 ( 1 − y ) 2 3 ] 2 1 1 = ( 2 ⋅ 3 2 ⋅ ( 2 1 ) 2 3 − 0 ) + ( 0 − ( − 2 ⋅ 3 2 ⋅ ( 2 1 ) 2 3 ) ) = 3 4 ⋅ 2 2 1 + 3 4 ⋅ 2 2 1 = 3 2 2 + 3 2 2 = 3 2 2 Qual o volume do conjunto abaixo?
C = { 0 < z < 1 ∧ x 2 + y 2 < z 2 } C = \{0 < z < 1 \land x^2+y^2 < z^2\} C = { 0 < z < 1 ∧ x 2 + y 2 < z 2 }
Fixando primeiro z z z
Volume = ∫ 0 1 A ˊ rea ( z ) d z \text{Volume} = \int^1_0 \text{Área}(z) \d z Volume = ∫ 0 1 A ˊ rea ( z ) d z
A ˊ rea ( z ) = ∫ − z z ( ∫ − z 2 − x 2 z 2 − x 2 1 d y ) d x Volume = ∫ 0 1 ( ∫ − z z ( ∫ − z 2 − x 2 z 2 − x 2 1 d y ) d x ) d z \begin{darray}{l}
\text{Área}(z) = \int^z_{-z}\left(\int^{\sqrt{z^2-x^2}}_{-\sqrt{z^2-x^2}} 1 \d y \right) \d x\\
\text{Volume} = \int^1_0\left( \int^z_{-z}\left(\int^{\sqrt{z^2-x^2}}_{-\sqrt{z^2-x^2}} 1 \d y \right) \d x \right) \d z
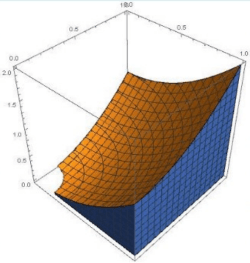
\end{darray} A ˊ rea ( z ) = ∫ − z z ( ∫ − z 2 − x 2 z 2 − x 2 1 d y ) d x Volume = ∫ 0 1 ( ∫ − z z ( ∫ − z 2 − x 2 z 2 − x 2 1 d y ) d x ) d z Qual o volume de { 0 ≤ z ≤ x 2 + y 2 ∧ 0 ≤ x , y ≤ 1 } \{0 \leq z \leq x^2+y^2 \land 0 \leq x,y \leq 1\} { 0 ≤ z ≤ x 2 + y 2 ∧ 0 ≤ x , y ≤ 1 }
Fixando x x x 0 ≤ x ≤ 1 0 \leq x \leq 1 0 ≤ x ≤ 1
0 ≤ z ≤ x 2 + y 2 , 0 ≤ y ≤ 1 0 \leq z \leq x^2+y^2 \quad, \quad 0 \leq y \leq 1 0 ≤ z ≤ x 2 + y 2 , 0 ≤ y ≤ 1
Fixando de seguida y y y g g g
Volume = ∫ 0 1 ( ∫ 0 1 ( ∫ 0 x 2 + y 2 1 d z ) d y ) d x \text{Volume} = \int^1_0\left( \int^1_0 \left( \int^{x^2+y^2}_0 1 \d z \right) \d y \right) \d x Volume = ∫ 0 1 ( ∫ 0 1 ( ∫ 0 x 2 + y 2 1 d z ) d y ) d x Existem mais exemplos nos slides da aula 20
Slides: