Sucessões
DEFINIÇÃO
- Sucessão limitada: O conjunto dos seus termos é limitado, isto é, é uma sucessão majorada e minorada.
- Sucessão monótona: Quando uma sucessão é (estritamente) crescente ou (estritamente) decrescente. Por outras palavras, quando ou , respetivamente.
Operações com sucessões
Podemos efetuar as seguintes operações com sucessões:
- multiplicar por um escalar
- somar e subtrair duas sucessões
- multiplicar duas sucessões
- dividir duas sucessões (com atenção de que o denominador nunca pode ser zero).
Também podemos, para uma sucessão real positiva, e , efetuar e .
Sub-sucessões
Seja () uma sucessão de números reais e () uma sucessão estritamente crescente de números naturais positivos. Chama-se à sucessão de termo geral uma sub-sucessão de ().
Exemplo 1
Exemplo 2
Utiliza-se as sub-sucessões para conseguir mais facilmente estudar uma sucessão, devido às seguintes propriedades:
- Qualquer sub-sucessão de uma sucessão limitada é também limitada.
- Qualquer sub-sucessão de uma sucessão monótona tem a mesma monotonia que a sucessão original.
- Se uma família de sub-sucessões de uma mesma sub-sucessão é tal que a reunião dos seus termos é igual ao conjunto dos termos da sucessão original então se todas as sub-sucessões dessa família forem limitadas a sucessão original também o é.
- Se duas sub-sucessões de uma mesma sucessão tiverem monotonias diferentes a sucessão original não é monótona. O mesmo se pode concluir se qualquer sub-sucessão da sucessão original não for monótona, evidentemente.
Existência de sub-sucessões monótonas para qualquer sucessão
TEOREMA
Existência de sub-sucessões monótonas para qualquer sucessão
Seja () uma sucessão de números reais, então () tem, pelo menos, uma sub-sucessão monótona (isto é, crescente ou decrescente)
Por exemplo, a sucessão não é monótona (é alternadamente positiva e negativa).
No entanto, as sub-sucessões
são, respetivamente, crescente e decrescente.
É sempre possível encontrar uma sub-sucessão que seja monótona.
A justificação para tal encontra-se no PDF em anexo (aula 4).
É também importante relembrar que uma sucessão constante (e.g. ) também é monótona.
Sucessão convergente
Uma sucessão convergente é uma sucessão em que existe limite. Por outras palavras, significa que para uma ordem suficientemente grande (ou seja, ou ), existe uma vizinhança para qualquer a que pertencem os termos de .
Qualquer sucessão que não seja convergente é divergente.
É também fácil de perceber que uma sucessão constante , é convergente.
Exemplo
Considerando a sucessão , podemos provar que é convergente:
Então,
Logo, para qualquer tem-se .
Infinitésimo: Diz-se que uma sucessão () é um infinitésimo se
TEOREMA
Limitação das sucessões convergentes
Seja () uma sucessão convergente, então () é limitada.
Atenção que o contrário nem sempre se verifica.
Comportamento da relação de ordem na passagem ao limite: Sejam () e () duas sucessões convergentes, tem-se:
- Se então para
- Se para então
- Se para então
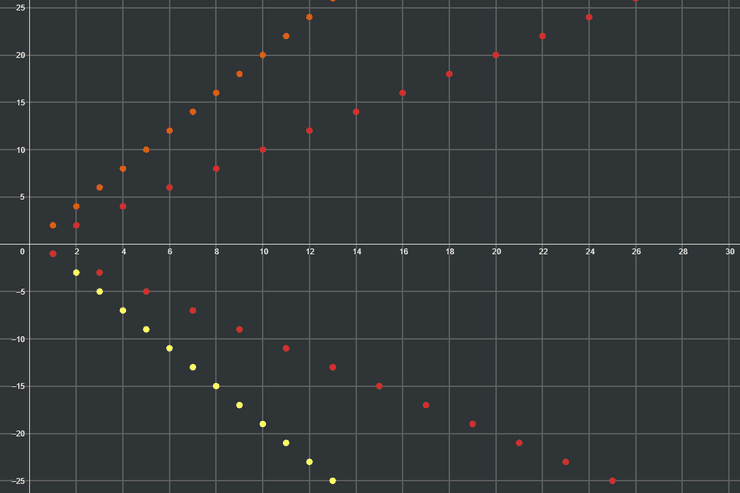
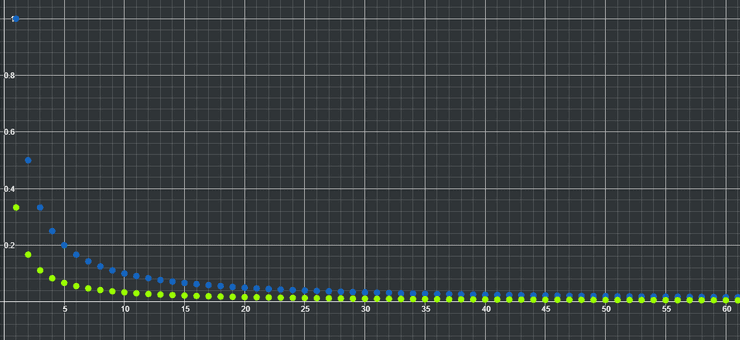
Esta última propriedade pode-se exemplificar através das seguintes sucessões, representadas no gráfico:
e
Podemos intuitivamente perceber que . No entanto, ambas as sucessões tendem para zero, isto é, .
TEOREMA
Convergência das sub-sucessões das sucessões convergentes
Seja () uma sucessão convergente, então qualquer sub-sucessão de () é convergente para .
DEFINIÇÃO
Sublimite de uma sucessão
Diz-se que é um sublimite de () se existe uma sub-sucessão de (), (), tal que .
De acordo com esta última definição:
- Se existir uma sub-sucessão nas condições da definição, existe um número infinito delas
- Qualquer sucessão convergente só tem um sublimite (que é o limite da sucessão)
TEOREMA
Convergência das sucessões monótonas e limitadas
Seja () uma sucessão de números reais que é monótona e é limitada, então () é convergente.
Propriedades operatórias com limites
Assumindo que e :
- (ver exceções na página 7 do PDF da aula 4 em anexo)
- , sendo que e
Sucessões definidas por recorrência
Uma sucessão pode estar definida sem ser pelo seu termo geral .
Outra forma de definir uma sucessão é por recorrência. Por exemplo:
Nestas sucessões não é tão fácil determinar a sua monotonia, se é convergente ou não e, consequentemente, o seu limite. Nestes casos é importante recorrer à Indução Matemática.
Vejamos como determinar a monotonia da sucessão acima. Começamos ver os valores de e , de forma a percebermos se a sucessão irá ser crescente ou decrescente.
Logo, se a sucessão for monótona, terá de ser crescente. Indo agora para a indução matemática, começamos por averiguar a base:
A etapa de indução é:
Logo, podemos concluir que a sucessão é estritamente crescente.
Para descobrirmos se a sucessão é convergente apenas precisamos de descobrir se é majorada, visto que é crescente. No entanto, como a sucessão está definida por recorrência, podemos tentar "adivinhar" um valor para a qual esta seja majorada. Conseguimos intuitivamente perceber que . Como tal, podemos recorrer à indução matemática para o provar:
Logo, como a condição se prova para a base e é hereditária, conseguimos comprovar que a sucessão é majorada, logo é convergente. Infelizmente, isto não nos permite determinar . No entanto, ao saber que a sucessão é convergente, podemos usar um método que nos permite descobrir .
Como sabemos que () é uma sub-sucessão de () e que , podemos obter o valor de :
Teorema de Bolzano-Weierstrass
Teorema
Teorema de Bolzano-Weierstrass
Seja () uma sucessão limitada, então () tem pelo menos uma sub-sucessão convergente.
É fácil provar isto, se, tal como definido anteriormente, pensarmos que qualquer sucessão tem, pelo menos, uma sucessão monótona. Ora, se uma sucessão é monótona e limitada, então é convergente.
Teorema das Sucessões Enquadradas
Teorema
Teorema das Sucessões Enquadradas (TSE)
Sejam (), () e () sucessões de números reais tais que para ,
e e , para algum , então .
Exemplos do uso do teorema
Pretende-se descobrir o limite da sucessão
Como e são infinitésimos, isto é, tendem para zero, podemos concluir que .
Teorema
Corolário do Teorema das Sucessões Enquadradas
Qualquer produto de uma sucessão limitada por um infinitésimo é um infinitésimo.
Aplicação do TSE a sucessões definidas por somatórios
Seja
queremos determinar o limite desta sucessão.
Para tal, comecemos por construir o enquadramento da sucessão. Para tal, vamos utilizar a expressão no interior do somatório. Dado que, para qualquer tal que , se tem:
Podemos agora continuar a "construir" o enquadramento, adicionando os somatórios:
Como o valor de um somatório em que a expressão no seu "interior" não contenha é vezes a expressão no seu "interior", temos que:
Podemos agora determinar o limite de ambas as sucessões:
Logo, pelo Teorema das Sucessões Enquadradas, .
Sucessão de Cauchy
Definição
Sucessão de Cauchy
Seja () uma sucessão de números reais, diz-se que () é uma sucessão de Cauchy se, para qualquer real positivo ,
para .
Por outras palavras, isto significa que, para uma ordem e infinitamente grandes, o módulo da diferença entre os termos e deverá ser arbitrariamente pequena.
Teorema
Convergência das sucessões de Cauchy
Seja () uma sucessão de números reais, então () é convergente se e só se é uma sucessão de Cauchy.
No PDF da Aula 5 em anexo, páginas 8-9, encontra-se um exemplo de como averiguar se uma sucessão é uma sucessão de Cauchy.
Sucessão contrativa
Definição
Sucessão contrativa
Seja () uma sucessão de números reais, diz-se que () é contrativa se existir uma constante tal que:
Outra maneira mais simples de definir uma sucessão contrativa é dizer que, a partir de certa ordem (), a distância entre dois termos consecutivos diminui com uma taxa de contração não superior a , tornando-se assim, muito pequena.
Teorema
Convergência das sucessões contrativas
Seja () uma sucessão contrativa de números reais, então () é convergente.
Verificar se uma sucessão é contrativa
Tomemos como exemplo a sucessão
Atendendo à definição de sucessão contrativa, podemos escrever o seguinte:
Sabemos que para , , de acordo com a sua expressão. Logo, conseguimos deduzir que (relembro que ao inverter, o sinal da inequação se altera). Daqui vem que:
Logo, como , a sucessão é contrativa, sendo consecutivamente convergente.
Como é convergente, podemos dizer que se então , pois trata-se de uma sub-sucessão. Podemos assim determinar o limite da sucessão:
Como sabemos que a sucessão só tem termos positivos para , podemos concluir que .
PDFs: